Good Mood

Zobrazit Mobilní Oznámení, Zobrazit Všechny Poznámky, Skrýt Všechny Poznámky,

Část 4-6 : Tvar Grafu, Část II

V předchozí části jsme viděli, jak bychom mohli pomocí první derivace funkce získat nějaké informace o grafu funkce. V této části se podíváme na informace, které nám druhá derivace funkce může poskytnout o grafu funkce.

než to uděláme, budeme potřebovat několik definic z cesty. Hlavní koncept, o kterém budeme diskutovat v této části, je konkávnost. Konkávnost je nejjednodušší vidět s grafem(dáme matematickou definici v bit).,

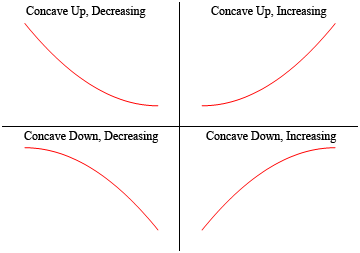
Takže, funkce je konkávní, pokud to „otevře“ a funkce je konkávní dolů, pokud to „otevře“. Všimněte si také, že konkávnost nemá nic společného se zvyšováním nebo snižováním. Funkce může být konkávní nahoru a buď zvýšení nebo snížení. Podobně může být funkce konkávní dolů a buď se zvyšuje nebo snižuje.

pravděpodobně to není nejlepší způsob, jak definovat konkávnost tím, že řekne, jakým způsobem se „otevírá“, protože se jedná o poněkud mlhavou definici. Zde je matematická definice konkávnosti.,

Definice 1

ukázat, že grafy ve skutečnosti mají konkávní tvrdil výše, zde je graf opět (vyhodit do povětří trochu, aby se věci jasnější).

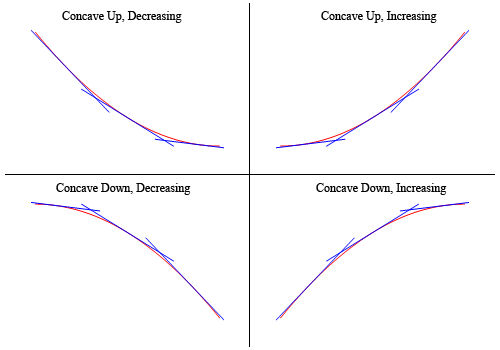
Takže, jak vidíte, ve dvou horních grafů všechny tečny v hrubých rysech jsou všechny pod grafem funkce a tyto jsou konkávní. Ve spodních dvou grafech jsou všechny tečny nad grafem funkce a ty jsou konkávní dolů.,

znovu si všimněte, že konkávnost a zvyšující se/klesající aspekt funkce jsou zcela oddělené a nemají nic společného. To je důležité si uvědomit, protože studenti tyto dva často míchají a používají informace o jednom k získání informací o druhém.

je tu ještě jedna definice, kterou musíme dostat z cesty.

Definice 2

nyní, když máme všechny definice konkávnosti z toho, jak potřebujeme přivést druhou derivaci do mixu. Nakonec jsme začali tuto sekci říkat, že použijeme druhou derivaci, abychom získali informace o grafu. Následující skutečnost souvisí s druhou derivací funkce s její konkávností. Důkazem této skutečnosti je důkaz z derivátových aplikací v kapitole Extras.

Takže, co tato skutečnost nám říká, že inflexní body budou všechny body byly druhá derivace změní znaménko., V předchozí kapitole jsme viděli, že funkce může změnit znaky, pokud je buď nulová, nebo neexistuje. Všimněte si, že jsme pracovali s první derivace v předchozí části, ale skutečnost, že funkci, případná změna známky, kde je nulová, nebo neexistuje, nemá nic společného s první derivace. Je to prostě fakt, který se vztahuje na všechny funkce bez ohledu na to, zda jsou deriváty nebo ne.,

to nám zase říká, že seznam možných inflexních bodů bude těch bodů, kde je druhý derivát nulový nebo neexistuje, protože to jsou jediné body, kde by druhý derivát mohl změnit znaménko.

buďte však opatrní, abyste nepředpokládali, že právě proto, že druhý derivát je nulový nebo neexistuje, že bod bude inflexním bodem. Budeme vědět, že se jedná o inflexní bod, jakmile určíme konkávnost na obou stranách. Bude to pouze inflexní bod, pokud se konkávnost liší na obou stranách bodu.,

Teď, když víme o konkávnost můžeme použít tyto informace, stejně jako zvýšení/snížení informace z předchozí části, získat docela dobrou představu o tom, jaký graf by měl vypadat. Podívejme se na příklad toho.

předchozí příklad můžeme použít k ilustraci jiného způsobu klasifikace některých kritických bodů funkce jako relativních maxima nebo relativních minima.

jak uvidíme, budeme muset být velmi opatrní s \(x = 0\)., V tomto případě je druhý derivát nula, ale to ve skutečnosti neznamená, že \(x = 0\) není relativní minimum nebo maximum. Některé příklady toho uvidíme za chvíli, ale musíme se nejprve postarat o další informace.

zde je také důležité poznamenat, že všechny kritické body v tomto příkladu byly kritickými body, ve kterých byl první derivát nulový, a to je nutné, aby to fungovalo. Tento test nebudeme moci použít v kritických bodech, kde derivát neexistuje.,

zde je test, který lze použít ke klasifikaci některých kritických bodů funkce. Důkaz tohoto testu je v sekci Doklady o derivátových aplikacích v kapitole Extras.

Test druhého derivátu

je důležité si všimnout třetí části druhého derivátového testu. Pokud je druhá derivace nulová, pak kritický bod může být cokoli. Níže jsou grafy tří funkcí, z nichž všechny mají kritický bod \(x = 0\), druhá derivace všech funkcí je nula na \(x = 0\) a přesto všechny tři možnosti jsou vystaveny.,

první je graf \(f\left (x \right) = {x^4}\). Tento graf má relativní minimum na \(x = 0\).

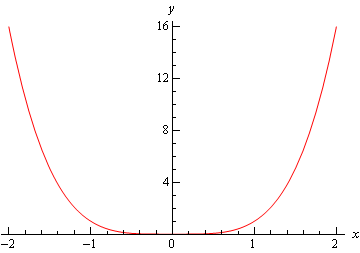
Další je graf funkce \(f\left( x \right) = – {x^4}\), který má relativní maximálně na \(x = 0\).

Konečně, tam je graf \(f\left( x \right) = {x^3}\) a tento graf se ani relativní minimální nebo maximální relativní v \(x = 0\).

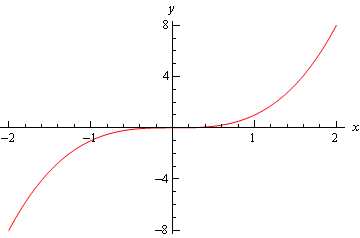
takže můžeme vidět, že musíme být opatrní, pokud spadáme do třetího případu., Pro ty časy, kdy se dostaneme do tohoto případu, se budeme muset uchýlit k jiným metodám klasifikace kritického bodu. To se obvykle provádí při prvním derivačním testu.

pojďme se vrátit a podívat se na kritické body z prvního příkladu a pokud možno použít druhý derivační Test.

pojďme pracovat ještě jeden příklad.