Good Mood

představte si to: Jste prezentaci vašeho Ph.d. práce o stabilitě na jednom ze seminářů. Všechno jde hladce a konečně je čas na otázky! A někdo z ničeho nic se ptá: „Jaký je rozdíl mezi implicitním a explicitním přístupem?”! A protože děláte statickou stabilitu … nikdy jste neslyšeli tyto podmínky! Jo… to už se stalo!, Teď jsem trochu moudřejší, tak se pojďme podívat blíže na rozdíly mezi Implicitní a Explicitní analýzu

Implicitní a Explicitní analýzu se liší v přístupu k času inkrementace. V implicitní analýze pokaždé přírůstek musí konvergovat, ale můžete nastavit poměrně dlouhé časové přírůstky. Explicitní na druhé straně nemusí konvergovat každý přírůstek, ale aby bylo řešení přesné časové přírůstky, musí být velmi malé.

to zní docela jednoduše, že?, Pokud nezačnete přemýšlet o věcech, jako je „který z nich bych měl použít“ nebo „jak malý by měl být explicitní časový přírůstek“ a podobné věci. Bez obav,kryju tě!

pojďme se ponořit!

dynamika v celé své kráse-implicitní / explicitní!

k řešení dynamických problémů použijete implicitní a explicitní řešitele. To znamená, že nebudete muset znát tyto věci, pokud děláte statickou analýzu., Pokud si nejste jisti rozdílem mezi statickou a dynamickou analýzou, přečtěte si tento příspěvek nejprve-usnadní vám to pochopení!

Dynamická analýza v kostce:

Dynamická analýza řeší problémy zahrnující setrvačné účinky. Ty se objeví, když se věci rychle mění ve vašem modelu(rychle aplikované zatížení, nárazy atd.). Inženýři to obvykle přepočítávají jako „nelineární dynamika“.

je třeba poznamenat, že často inženýři nazývají i jinou analýzu „dynamickou“., Věci jako modální analýza nebo analýza nucené odezvy, které se zabývají vibracemi. Někdy se nazývají „lineární dynamika“, ale obvykle je dobré se ujistit, co někdo znamená, když používá takovou frázi. Zatímco „lineární dynamické“ problémy jsou opravdu zajímavé, nebudu diskutovat o nich zde. Můžete se dozvědět více o nich čtení tohoto příspěvku!

první věc, kterou opravdu cítím, musím zdůraznit, že implicitní a explicitní řešitelé řeší stejné problémy!, Přemýšlejte o tom ne jako o „různých řešitelích“, ale spíše o dvou různých způsobech řešení stejného problému.

v mnoha případech můžete použít implicitní i explicitní řešitel a budou mít stejný výsledek. A myslím, že tady musíme začít!

jak dynamická analýza funguje?

obě analýzy řeší problém, kde je důležitá rychlost věcí. To většinou znamená, že zatížení je aplikováno velmi rychle. V takových případech budete vždy“ iterovat “ zatížení včas., V zásadě využijete čas k tomu, abyste řešiteli řekli „co se děje“ a jak se mění zatížení.

nejprve musíte definovat, jak se zatížení mění v čase. Obvykle to děláte pomocí grafů, jako je ten níže:

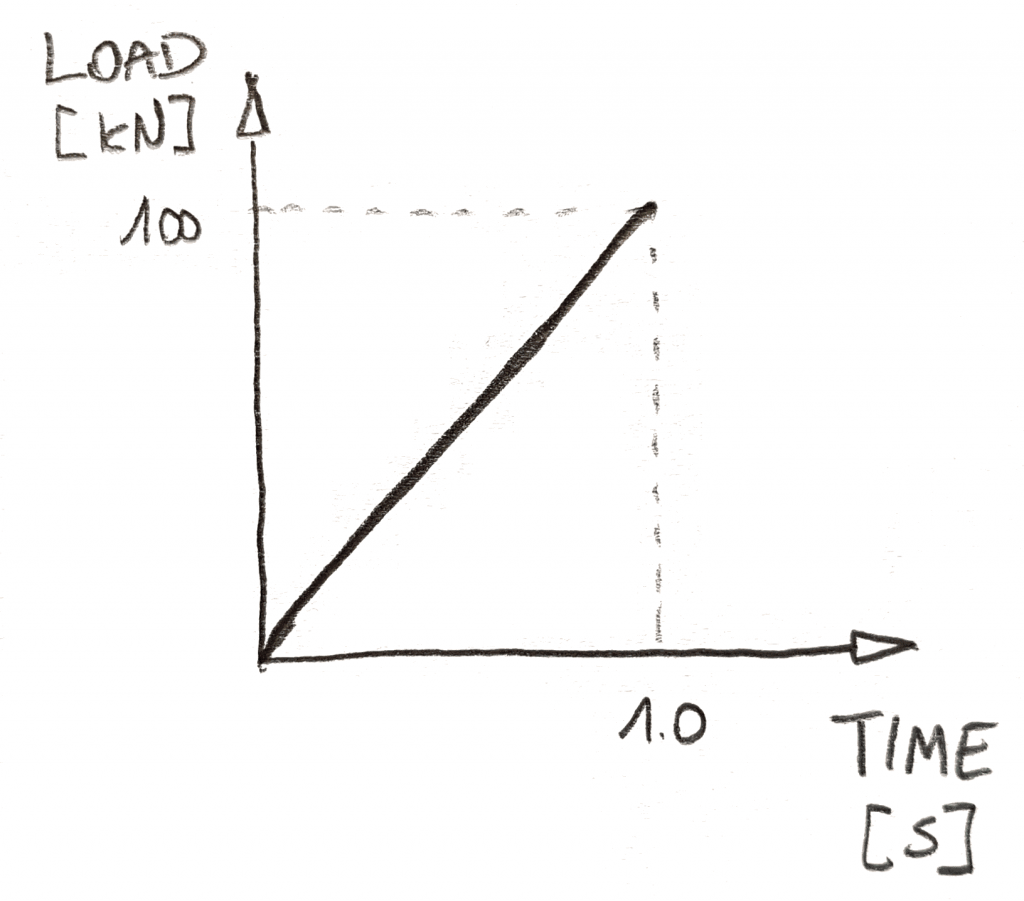
v nelineární dynamické analýze má čas 2 role. Za prvé, umožňuje vám říct řešiteli, kdy by mělo být aplikováno velké zatížení. Jednoduše musíte implementovat každé zatížení grafem závislým na čase. Za druhé … čas je čas! Říká řešiteli, jak rychle to jde!,

Představte si, že chcete mít takové zatížení pořadí:

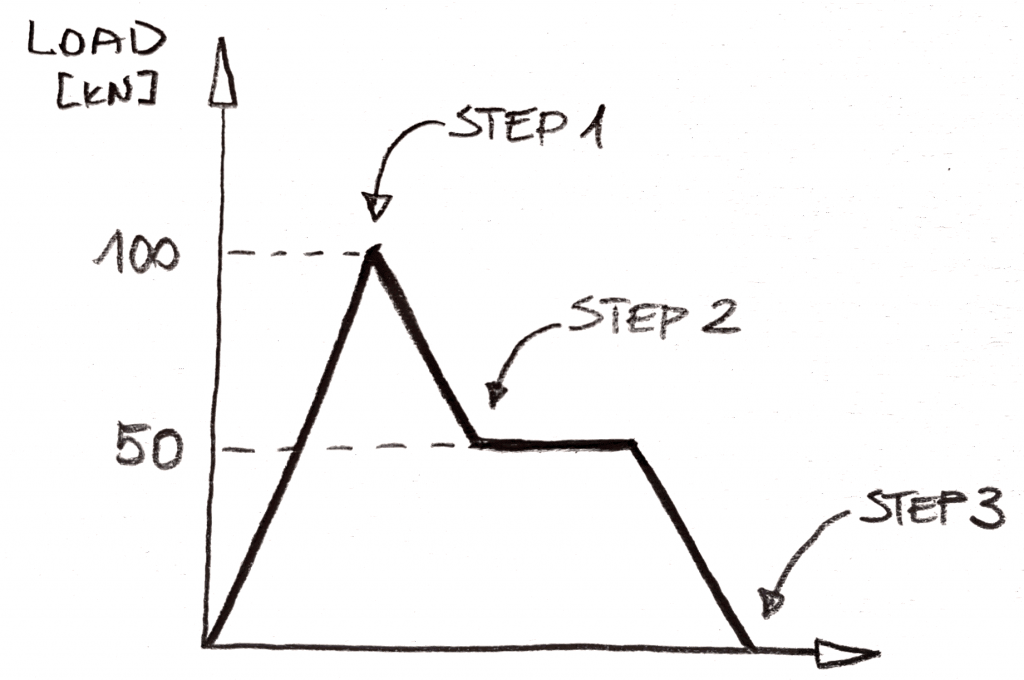
V statickém by toto bylo 3 „kroky“ analýza (ty se nazývají subcases v NX Nastran, ale myslím, že Abaqus vlastně použít „krok“, jako název, nemůžu si vzpomenout na to, pro jistotu, i když!). Myšlenka by byla jednoduchá, musíte použít 100kn zatížení v kroku 1, poté odstranit 50KN zátěže v kroku 2 a odstranit 50KN v kroku 3. Neexistuje žádný způsob, jak zahrnout „plošinu“ zatížení po kroku 2 do analýzy a bude vynechána., Logika je jednoduchá: žádné změny v zatížení = nic se nemění staticky!

přírůstků Zatížení ve statických

Pokud by problém být vysoce nelineární, zatížení by „zvýší“. Je vzácné použít “ plné zatížení „do nelineární analýzy na“one go“! Obvykle by řešitel platil tj. 1KN každý „přírůstek“. To znamená, že po 100 krocích bude použito plné zatížení kroku 1. To usnadňuje řešiteli konvergovat správnou odpověď.,

jako uživatel, dostanete definovat, jak velké přírůstky řešitel by měl používat. Existují také některé algoritmy pro změnu přírůstku zatížení během analýzy. Různí řešitelé chtějí, abyste to nastavili různými způsoby. Balíčky FEA obvykle používají multiplikátory zatížení. To znamená, že můžete říci něco jako:“v každém přírůstku použít další 0,01 veškerého zatížení“.

úžasné … ale pojďme k dynamice, můžeme?, V dynamické analýze můžete získat rozložení zatížení jako výše, s takovým nákladem definice:

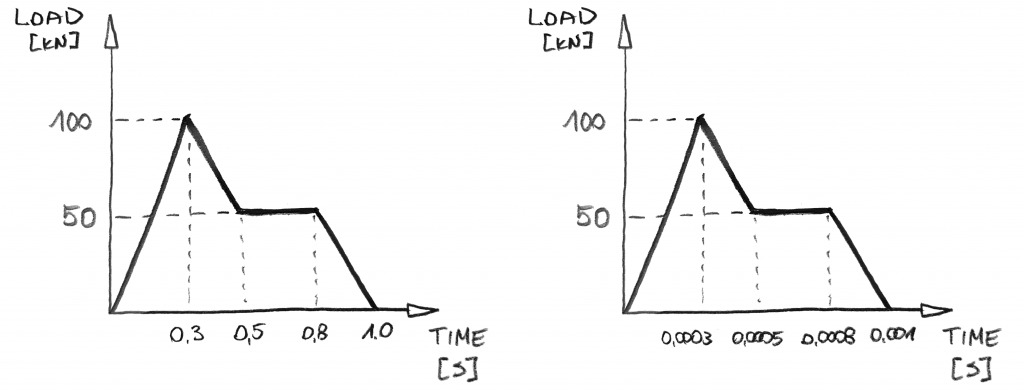
Okamžitě, existuje několik věcí, které si lze všimnout:

• nejsou Tam žádné kroky! Je to proto, že v dynamické analýze nebudete zvyšovat zatížení. Budete zvyšovat čas! A protože čas jde “ neustále „z nuly na předepsanou hodnotu, můžete jej zvýšit v“jednom kroku“.

• čas je podstatou! Pokud jde o hodnoty zatížení, výše uvedené grafy jsou stejné., Ale to není stejný dynamický případ! Graf vpravo aplikuje zatížení 1000x rychleji! To není něco, co můžete jen ignorovat v dynamické analýze!

obecně platí, že pokud chcete vyřešit dynamický problém, žádáte svého řešitele, aby udělal jednu věc. Požádáte ji, aby vypočítala řadu časových přírůstků, aby zjistila, co se v modelu děje. V každém z těchto přírůstků se čas mírně zvyšuje. To samozřejmě také mění zatížení modelu. To je důvod, proč musíte mít časově závislý graf pro zatížení., Takže řešitel „ví“, jaké zatížení by mělo být aplikováno v té době. V tomto rozsahu funguje stejně jako přírůstek zatížení ve statické analýze. Bonusem je, že vzhledem k tomu, že zvyšujete čas, mohou být vzaty v úvahu setrvačné účinky, když se věci dějí dostatečně rychle.

v tomto rozsahu implicitní i explicitní analýza dělá víceméně totéž. Rozdělují „čas analýzy“ na malé přírůstky a poté analyzují, co se děje ve vašem modelu jeden přírůstek času za druhým. Ale tady končí podobnosti!, Vidíte, existují odlišné přístupy k časové inkrementaci, kterou můžete mít!

implicitní vs explicitní – když čas opravdu záleží!

právě Jsi se dozvěděl, že za účelem výpočtu nelineární dynamický problém, budete muset postupně zvýšit „čas analýzy“. Jak jsem již zmínil, lze to provést dvěma způsoby.

začnu implicitním přístupem. Myslím, že je to snazší pochopit, protože to funguje víceméně stejně jako zvýšení zatížení v nelineární statické analýze!,

Jak implicitní analýza funguje:

nejprve se implicitní zdá být „základním“ řešením. V podstatě to funguje stejně, jak byste si mysleli, že by to mělo!

• Za prvé, při každém zvýšení „globální rovnováhy“ v modelu je stanovena. To znamená, že každý přírůstek musí konvergovat (to se děje v iteracích).

• poté, co je globální rovnováha v pořádku, solver vypočítá všechny lokální proměnné konečných prvků (napětí atd.) pro tento přírůstek.,

• výhody: vzhledem k tomu, že globální rovnováha je ověřena při každém přírůstku, mohou být tyto přírůstky velké!
• nevýhody: pokaždé, když přírůstek počítá pomalu, protože iterace jsou potřebné k dosažení globální rovnováhy.

Pokud jste obeznámeni s nelineární statickou analýzou, budete se cítit „doma“ s implicitním řešitelem. Jako uživatel obvykle řeknete, jak velké časové přírůstky chcete mít. To je obrovská výhoda… kterou lze snadno minout., Protože explicitní řešitel nenabízí takovou možnost!

pojďme se podívat na explicitní inkrementaci další!

jak explicitní analýza funguje:

tento je funky. Funguje to tak, že nemusíte konvergovat každý krok! Neexistují žádná konvergenční kritéria pro kontrolu a … žádné iterace! Místo ověření „globální rovnováhy“ řešitel předpokládá, že rovnováha „prostě existuje“. To znamená, že řešitel jde přímo do výpočtu místních konečných prvků proměnných!, Protože tento postup má pouze jeden krok:

• Vypočítejte všechny lokální konečných prvků proměnné pro daný přírůstek, a přesunout na další jeden!

• výhody: každý přírůstek počítá velmi rychle!
• nevýhody: aby to fungovalo, musí být časový krok extrémně malý. V opačném případě není možné udržet tuto rovnováhu, o které se předpokládá, že „prostě existuje“. K dosažení tohoto cíle, Uživatel nemají přímou kontrolu nad tím, jak Big-time přírůstky explicitní Řešitel bude trvat., Řešitel sám vypočítá, jak malé časové úseky jsou stále v pořádku. A ty přijatelné časové přírůstky jsou velmi malé! To je důvod, proč explicitní problémy by měly trvat zlomky druhé! Pokud by vydržely vteřiny … budete potřebovat miliony přírůstků!

pro rychlé shrnutí: implicitní i explicitní řešitelé řeší stejné věci. Jediný rozdíl je, jak tyto metody zvyšují čas.

technicky by oba měli mít pro všechny případy stejný výsledek., Koneckonců, můžete analyzovat stejný problém s oběma přístupy. Odpověď samozřejmě nemůže záviset na metodě použité k vyřešení problému! Ale samozřejmě si vyberete pouze jeden z přístupů pro váš další problém, takže který z nich? Pojďme to zjistit!

co je pro vás lepší: implicitní nebo explicitní?

už Jsme se shodli, že můžete použít jak implicitní a explicitní řešiče řešit stejný typ problémů. Jediný rozdíl je v přístupu k časové inkrementaci. Ale to není triviální věc!, Pokud by byl rozdíl malý, nikdo by se nestaral implementovat oba! Pojďme se tedy podívat na to, jak tentokrát přírůstková vliv věci!

implicitní i explicitní řešitelé mají některé oblasti, kde svítí. A jejich použití se překrývá:

• implicitní analýza umožňuje vybrat, jak velký by měl být časový přírůstek! Tento přírůstek bude nějakou dobu trvat, než se vypočítá, protože musí nejprve iterovat pro globální rovnováhu. Ale můžete to udělat „přiměřeně velké“ pro vaši analýzu.,

• explicitní časové přírůstky vypočítat opravdu rychle! Jednoduše proto, že nemají iteraci pro globální rovnováhy… ale čas přírůstek tam není vaše volba! Řešitel jednoduše předpokládá, že“ přijatelný „časový přírůstek je“ X “ a jde s ním. Všimněte si, že toto „X“ může být snadno něco jako 5e-7s … to je super malé! Chcete-li vyřešit problém, který se děje přes 1s, budete potřebovat 2 000 000 přírůstků!

• a to je vše! Rychlost výpočtu je přesně rozdíl mezi implicitní a explicitní., Velikost explicitního kroku samozřejmě závisí na vašem modelu a době výpočtu závisí na vašem hardwaru. Existují však pozorování, která můžeme snadno udělat:

Použít implicitní „pomalý analýzy“!

pokud se věc, kterou vypočítáte, stane během několika sekund… nemá smysl používat explicitní řešitel. To bude trvat věčně kopat přes miliony časových přírůstků potřebných pro to spočítat!, Místo toho nastavte“ přiměřený “ časový krok pro implicitní analýzu (řekněme 100 stejných časových přírůstků pro vaši analýzu). Jistě, každý z těchto implicitních časových přírůstků bude počítat mnohem déle než jeden explicitní přírůstek. Ale ne déle než stovky tisíc z nich!

Použití explicitní pro „rychlá analýza“!

to je zřejmé, že? Pokud se to, co vypočítáte, stane v malém zlomku sekundy explicitní, je váš přítel., V implicitní analýze by váš časový přírůstek byl velmi malý … možná i tak malý jako přírůstek v explicitní analýze. V takovém případě bude explicitní analýza probíhat mnohem rychleji, protože nevyžaduje iterace „global equilibrium“. Implicitní analýza vyžaduje tyto iterace (bez ohledu na časový krok!).

Mezi námi věci!

samozřejmě existují problémy, které se dějí uprostřed (jako dopad s rychlostí 5m/s)., Obvykle můžete vyřešit takový problém s oběma řešiteli, ale může to být nepříjemné.

doufám, že vám to pomůže vybrat správný přístup k vašim dynamickým problémům. Samozřejmě, na konci, zkušenost je nejlepší průvodce! Pokud máte pochybnosti, spusťte několik typických problémů implicitně i explicitně. Tímto způsobem budete moci porovnat výsledky (měly by být stejné). Ale co je důležitější, budete moci porovnat výpočetní časy! To vám dá příležitost zkontrolovat, jaký je pro vás lepší přístup!,

jak explicitní odhady velikosti kroku času?

No, to je všechno hezké a dandy tak daleko, ale myslím, že to by bylo hezké, řešit jeden velký problém. A to je … pokud nevybíráte časový krok ve své explicitní analýze … tak kdo?

matematické vysvětlení by vyžadovalo diskusi o maximální přirozené frekvenci. Je to proto, že maximální“ stále přijatelný “ časový přírůstek je nepřímo úměrný maximální přirozené frekvenci. Takové výpočty lze samozřejmě provést., Výsledky závisí na síti modelu (kolik prvků existuje atd.). Ale nepůjdeme tam, a tam jsou 2 důvody, proč: za prvé, nemám rád matematiku (!). Za druhé, to není, jak to řešitelé nakonec dělají, i když je to „správná cesta“.

řešitel může samozřejmě vypočítat maximální přirozenou frekvenci, ale to trvá poměrně dlouho. A protože by to muselo být provedeno v každém explicitním časovém přírůstku (může jich být spousta!) … Jejda!, Naštěstí existuje způsob, jak tuto hodnotu pěkně odhadnout analýzou každého konečného prvku v systému Samostatně! Fyzikální interpretace tohoto odhadu (běžně používané v řešitelů) je:

Maximální přírůstek času v explicitní analýza:

přírůstek Času v explicitní analýzy je velmi krátká. Je to doba, ve které může elastická vlna (tj. nárazová vlna) procházet jediným konečným prvkem vašeho modelu. To je samozřejmě ověřeno pro všechny konečné prvky ve vašem modelu a je vybrán nejmenší čas.,

Jak můžete vidět, tam jsou 2 složky do explicitní časová složka:

• Elastické vlny rychlost (neboli rychlost zvuku ve vašem materiál)! To závisí pouze na materiálu, který máte ve svém modelu (a je to samozřejmě jiné pro různé materiály!). Budete potřebovat mladý modul E, hustotu materiálu a Poissonovu dávku (ve 2D a 3D problémech). Je snadné najít tabulky, které uvádějí rychlosti elastických vln v různých materiálech. Jen pro referenci v oceli je to kolem 5200m/s (mnoho kovů je kolem 4500-5500m / s).,

• velikost prvku (a kvalita)! Máte rychlost vlny, ale to nestačí! Chcete-li znát čas, který potřebuje k cestování přes prvek, musíte znát prvek „délka“. I když je to super jednoduché, ve 1D prvků (oni prostě mají délku) to dostane ošidné, v 2D a 3D. Tato délka není „prostě“ nejkratší hrany prvku od prvků může mít dost špatná geometrie. Existují věci, které řešitel dělá pro výpočet tohoto. Ve 2D by to mohla být oblast prvku dělená maximální délkou okraje., Ve 3D může znamenat, že objem prvku je dělen maximální boční plochou. To je důvod, proč nejen velikost prvku, ale také kvalita prvků je tak důležitá v explicitní analýze! Koneckonců … vše, co potřebujete, je jeden špatný prvek, který opravdu poškodí váš výpočetní čas!

někde jsem četl, že zatímco výše uvedené je „přesné“ řešení, řešitelé často používají „bezpečnostní faktory“. Pokud získáte vyšší časový přírůstek než elastická vlna, dojde k matematickým chybám „speed limit“. Vzhledem k tomu, že se používají odhady, řešitelé často zkracují časový krok „jen pro případ“., Obvykle je redukční faktor kolem 0,9, ale to se může samozřejmě lišit od řešitele k řešiteli.

mass scaling!

nakonec chci něco rychle zmínit.

pravděpodobně jste si všimli, že časový krok explicitně závisí pouze na síti, mladém modulu a hustotě. Snížení mladého modulu nemusí být samozřejmě ideální a často potřebujete malou síť k analýze detailů. Ale v“ nízkých dynamických “ problémech se můžete pokusit zvýšit explicitní časový krok zvýšením hustoty materiálu.,

toto se nazývá „mass scaling“. Balíčky FEA dokonce nabízejí řešení, kde se hustota zvyšuje pouze v prvcích, které“ rozhodují “ o zvýšení času. To znamená, že někdy jen malé části vašeho modelu těžší! V některých analýzách se můžete“ dostat pryč “ se zvýšením hmotnosti vašeho modelu. Pokud tomu tak je, může to být řešení pro vás. Jen si uvědomte, že to mění, jak se váš model chová! Pokud se jedná o vysoké zrychlení, je nejlepší být opatrný!

souhrn

Nice!, Dostal jsi se sem, díky za přečtení! Pojďme to zabalit, takže je snadnější si pamatovat!

• dynamická analýza zahrnuje čas! Když použijete zatížení, musí být definovány v časové funkci. Často se jedná o lineární vztah. To se však nemění, že čas, ve kterém je zatížení aplikováno, hraje významnou roli (zejména pokud je tento čas krátký!).

• 2 příchutě dynamické analýzy! „Skutečné“ dynamické problémy můžete vyřešit pomocí implicitních a explicitních algoritmů. Oba jsou v pořádku a ani jeden z nich není „lepší“., Ale měl bych říci, že explicitní Řešitel je součástí méně FEA balíčků. Protože ne každý balíček FEA má dokonce jeden, explicitní Řešitel je považován za“ pokročilejší “ věc.

• implicitní Řešitel je opravdu dobrý, pokud se věci ve vaší analýze dějí relativně pomalu. Řekněme, že analýza je delší než 1s, aniž by během té doby došlo k náhlým věcem. Výhodou je, že si můžete vybrat, jak velký časový přírůstek chcete. I když výpočet jednoho přírůstku trvá déle, je jich mnohem méně!,

• explicitní Řešitel je skvělý pro rychlé děje věcí (řekněme rychleji než 0.1 s). Zde si nevyberete časový přírůstek – řešitel jej automaticky nastaví. I když jsou obvykle velmi malé, alespoň počítají mnohem rychleji než „implicitní“. Explicitní řešitel vypočítá, jak velký by měl být časový přírůstek. To závisí na rychlosti zvuku ve vašem materiálu, minimální velikosti konečných prvků (a kvalitě prvků!). V některých případech můžete změnit hustotu (i automaticky pouze v „rozhodovacích prvcích“!) upravit tento časový přírůstek., To funguje, protože rychlost zvuku ve vašem materiálu závisí na jeho hustotě! Toto se nazývá „masové škálování“.