Biografía – Que fue Pascal

Blaise Pascal (1623-1662)
El Francés Blaise Pascal fue un destacado Siglo 17, científico, filósofo y matemático. Al igual que muchos grandes matemáticos, fue un niño prodigio y siguió muchas vías diferentes de esfuerzo intelectual a lo largo de su vida., Gran parte de sus primeros trabajos fueron en el área de las ciencias naturales y Aplicadas, y tiene una ley física que lleva su nombre (que «la presión ejercida en cualquier lugar de un líquido confinado se transmite por igual y sin disminuir en todas las direcciones a través del líquido»), así como la unidad internacional para la reducción de la presión. En filosofía, la apuesta de Pascals es su enfoque pragmático de creer en Dios sobre la base de que es una mejor «apuesta» que no hacerlo.
Pero Pascal también fue un matemático de primer orden., A la edad de dieciséis años, escribió un tratado significativo sobre el tema de la geometría proyectiva, conocido como Teorema de Pascal, que establece que, si un hexágono está inscrito en un círculo, entonces los tres puntos de intersección de lados opuestos se encuentran en una sola línea, llamada la línea de Pascal. Cuando era joven, construyó una máquina de cálculo funcional, capaz de realizar adiciones y sustracciones, para ayudar a su padre con sus cálculos de impuestos.,
Triángulo de Pascal
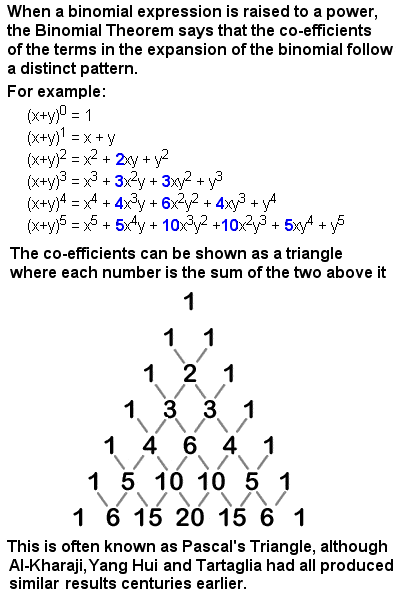
la tabla de coeficientes binomiales conocida como Triángulo de Pascal
Sin embargo, es mejor conocido por el Triángulo de Pascal, una conveniente presentación tabular de coeficientes binomiales, donde cada número es la suma de los dos números directamente encima de él. Un binomio es un tipo simple de expresión algebraica que tiene solo dos términos operados solo por adición, Resta, Multiplicación y exponentes positivos de números enteros, como (x + y)2., Los coeficientes producidos cuando un binomio se expande forman un triángulo simétrico (Ver imagen a la derecha).
Pascal estaba lejos de ser el PRIMERO en estudiar este triángulo. El matemático persa al-Karaji había producido algo muy similar ya en el siglo 10, y el triángulo se llama triángulo de Yang Hui en China después del matemático chino del siglo 13, y el Triángulo de Tartaglia en Italia después del italiano del siglo 16 epónimo., Pero Pascal contribuyó una prueba elegante mediante la definición de los números por recursión, y también descubrió muchos patrones útiles e interesantes entre las filas, columnas y diagonales de la matriz de números. Por ejemplo, mirando solo las diagonales, después de la «piel» exterior de 1, la siguiente diagonal (1, 2, 3, 4, 5,…) es los números naturales en orden. La siguiente diagonal dentro de eso (1, 3, 6, 10, 15,…) es los números triangulares en orden. El siguiente (1, 4, 10, 20, 35,…) es los números triangulares piramidales, etc, etc., También es posible encontrar números primos, números de Fibonacci, números catalanes y muchas otras series, e incluso encontrar patrones fractales dentro de ella.
Pascal también dio el salto conceptual de usar el triángulo para ayudar a resolver problemas en la teoría de la probabilidad. De hecho, fue a través de su colaboración y correspondencia con su contemporáneo francés Pierre de Fermat y el holandés Christiaan Huygens sobre el tema que nació la teoría matemática de la probabilidad., Antes de Pascal, no había una teoría real de la probabilidad-a pesar de la exposición temprana de Gerolamo Cardano en el siglo XVI-simplemente una comprensión (de una especie) de cómo calcular las «posibilidades» en los juegos de dados y cartas contando resultados igualmente probables. Algunos problemas aparentemente bastante elementales en la probabilidad habían eludido a algunos de los mejores matemáticos, o dado lugar a soluciones incorrectas.,
cayó a la de Pascal (con Fermat ayuda) para reunir a los diferentes subprocesos de conocimientos previos (incluyendo Cardano obra temprana) y para introducir completamente nuevas técnicas matemáticas para la solución de problemas que hasta ahora se habían resistido a la solución., Dos de estos problemas intransigentes a los que Pascal y Fermat se aplicaron fueron la ruina del jugador (determinar las posibilidades de ganar para cada uno de dos hombres que juegan un juego de dados en particular con reglas muy específicas) y el problema de los puntos (determinar cómo las ganancias de un juego deben dividirse entre dos jugadores igualmente hábiles si el juego se terminó prematuramente). Su trabajo sobre el problema de los puntos en particular, aunque no publicado en el momento, fue muy influyente en el desarrollo de nuevo campo.,
El Problema de los puntos

La solución de Fermat y Pascal al problema de los puntos
el problema de los puntos en su forma más simple se puede ilustrar con un simple juego de «winner take all» que implica el lanzamiento de una moneda. El primero de los dos jugadores (por ejemplo, Fermat y Pascal) en lograr diez puntos o victorias es recibir un bote de 100 Francos. Pero, si el juego se interrumpe en el punto donde Fermat, digamos, está ganando 8 puntos a 7, ¿Cómo se divide el bote de 100 Francos?, Fermat afirmó que, como solo necesitaba dos puntos más para ganar el juego, y Pascal necesitaba tres, el juego habría terminado después de cuatro lanzamientos más de la moneda (porque, si Pascal no obtuvo los 3 puntos necesarios para su victoria sobre los cuatro lanzamientos, entonces Fermat debe haber ganado los 2 puntos necesarios para su victoria, y viceversa. Fermat luego enumeró exhaustivamente los posibles resultados de los cuatro lanzamientos, y concluyó que ganaría en 11 de los 16 posibles resultados, por lo que sugirió que los 100 Francos se dividieran 11⁄16 (0,6875) a él y 5⁄16 (0,3125) a Pascal.,
Pascal entonces buscó una forma de generalizar el problema que evitara la tediosa lista de posibilidades, y se dio cuenta de que podía usar filas de su triángulo de coeficientes para generar los números, sin importar cuántos lanzamientos de la moneda permanecieran. Como Fermat necesitaba 2 puntos más para ganar el juego y Pascal necesitaba 3, se fue a la quinta fila (2 + 3) del triángulo, es decir. 1, 4, 6, 4, 1., Los primeros 3 términos sumados (1 + 4 + 6 = 11) representó los resultados donde Fermat ganaría, y los dos últimos términos (4 + 1 = 5) los resultados donde Pascal ganaría, del número total de resultados representados por la suma de toda la fila (1 + 4 + 6 +4 +1 = 16).
Pascal y Fermat habían captado a través de su correspondencia un concepto muy importante que, aunque quizás intuitivo para nosotros hoy en día, era casi revolucionario en 1654., Esta era la idea de resultados igualmente probables, que la probabilidad de que algo ocurriera podría calcularse enumerando el número de formas igualmente probables en que podría ocurrir, y dividiendo esto por el número total de posibles resultados de la situación dada. Esto permitió el uso de fracciones y ratios en el cálculo de la probabilidad de eventos, y la operación de multiplicación y adición en estas probabilidades fraccionales., Por ejemplo, la probabilidad de lanzar un 6 en un dado dos veces es de 1⁄6 x 1⁄6 = 1⁄36 («y» obras como la multiplicación); la probabilidad de lanzar un 3 o un 6 es 1⁄6 + 1⁄6 = 1⁄3 («o» funciona como la suma).
Más tarde en la vida, Pascal y su hermana Jacqueline se identificaron fuertemente con el movimiento religioso católico extremo del jansenismo. Tras la muerte de su padre y una » experiencia mística «a finales de 1654, tuvo su» segunda conversión » y abandonó por completo su trabajo científico, dedicándose a la filosofía y la teología., Sus dos obras más famosas, las «Lettres provinciales» y las «Pensées», datan de este período, Este último quedó incompleto a su muerte en 1662. Siguen siendo el legado más conocido de Pascal, y por lo general es recordado hoy como uno de los autores más importantes del período clásico francés y uno de los más grandes maestros de la prosa Francesa, mucho más que por sus contribuciones a las matemáticas.,
| << Back to Fermat | Forward to Newton >> |















