Mostrar Aviso móvil Mostrar todas las notas ocultar todas las notas
sección 4-6 : la forma de un gráfico, Parte II
en la sección anterior vimos cómo podríamos usar la primera derivada de una función para obtener información sobre el gráfico de una función. En esta sección vamos a ver la información que la segunda derivada de una función nos puede dar una sobre el gráfico de una función.
antes de hacer esto necesitaremos un par de definiciones fuera del camino. El concepto principal que discutiremos en esta sección es la concavidad. La concavidad es más fácil de ver con un gráfico(vamos a dar la definición matemática en un poco).,
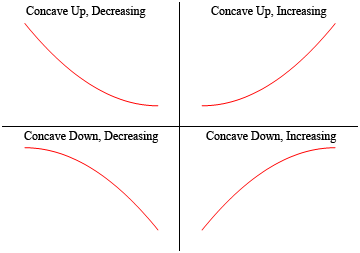
Así, una función es cóncava hacia arriba si se «abre» y la función es cóncava hacia abajo si se «abre» hacia abajo. Observe también que la concavidad no tiene nada que ver con aumentar o disminuir. Una función puede ser cóncava hacia arriba y aumentar o disminuir. Del mismo modo, una función puede ser cóncava hacia abajo y aumentar o disminuir.
probablemente no sea la mejor manera de definir la concavidad diciendo De qué manera «se abre», ya que esta es una definición algo nebulosa. Aquí está la definición matemática de concavidad.,
definición 1
para mostrar que los gráficos anteriores de hecho tienen concavidad reclamada aquí es el gráfico de nuevo (ampliada un poco para hacer las cosas más claras).
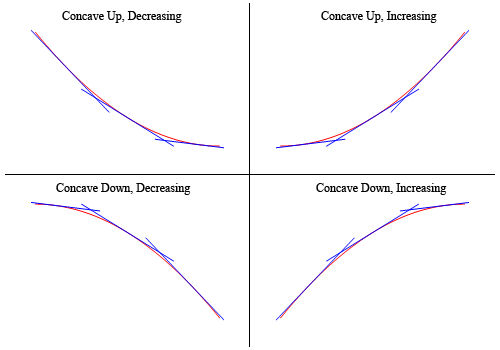
así que, como puede ver, en los dos gráficos superiores todas las líneas tangentes esbozadas están debajo del gráfico de la función y estas son cóncavas hacia arriba. En los dos gráficos inferiores todas las líneas tangentes están por encima de la gráfica de la función y estas son cóncavas hacia abajo.,
nuevamente, observe que la concavidad y el aspecto creciente/decreciente de la función están completamente separados y no tienen nada que ver entre sí. Es importante tener en cuenta esto porque los estudiantes a menudo mezclan estos dos y usan la información sobre uno para obtener información sobre el otro.
hay una definición más que necesitamos para salir del camino.
definición 2
un punto \(x = C\) se llama un punto de inflexión si la función es continua en el punto y la concavidad del gráfico cambia en ese punto.,
ahora que tenemos todas las definiciones de concavidad fuera del camino necesitamos traer la segunda derivada a la mezcla. Después de todo comenzamos esta sección diciendo que íbamos a usar la segunda derivada para obtener información sobre el gráfico. El siguiente hecho relaciona la segunda derivada de una función con su concavidad. La prueba de este hecho está en la sección Pruebas de aplicaciones derivadas del capítulo Extras.
hecho
así que, lo que este hecho nos dice es que los puntos de inflexión serán todos los puntos fueron el segundo signo de cambios derivados., Vimos en el capítulo anterior que una función puede cambiar signos si es cero o no existe. Tenga en cuenta que estábamos trabajando con la primera derivada en la sección anterior, pero el hecho de que una función posiblemente cambiando signos donde es cero o no existe no tiene nada que ver con la primera derivada. Es simplemente un hecho que se aplica a todas las funciones independientemente de si son derivadas o no.,
esto a su vez nos dice que una lista de posibles puntos de inflexión serán aquellos puntos donde la segunda derivada es cero o no existe, ya que estos son los únicos puntos donde la segunda derivada podría cambiar de signo.
tenga cuidado sin embargo de no hacer la suposición de que solo porque la segunda derivada es cero o no existe que el punto será un punto de inflexión. Solo sabremos que es un punto de inflexión una vez que determinemos la concavidad a ambos lados de él. Sólo será un punto de inflexión, si la concavidad es diferente en ambos lados del punto.,
ahora que sabemos sobre la concavidad podemos usar esta información, así como la información creciente/decreciente de la sección anterior para tener una idea bastante buena de cómo debería ser un gráfico. Echemos un vistazo a un ejemplo de eso.
Podemos usar el ejemplo anterior para ilustrar otra forma de clasificar algunos de los puntos críticos de una función como máximos relativos o mínimos relativos.
como veremos en un poco tendremos que tener mucho cuidado con \(x = 0\)., En este caso la segunda derivada es cero, pero eso no significa realmente que \(x = 0\) no es un mínimo relativo o máximo. Veremos algunos ejemplos de esto en un rato, pero necesitamos conseguir alguna otra información tomada cuidado de primero.
también es importante señalar aquí que todos los puntos críticos en este ejemplo eran puntos críticos en los que la primera derivada era cero y esto es necesario para que esto funcione. No podremos usar esta prueba en puntos críticos donde la derivada no existe.,
Aquí está la prueba que se puede utilizar para clasificar algunos de los puntos críticos de una función. La prueba de esta prueba se encuentra en la sección Pruebas de aplicaciones derivadas del capítulo Extras.
segunda prueba de derivada
es importante notar la tercera parte de la segunda prueba de derivada. Si la segunda derivada es cero entonces el punto crítico puede ser cualquier cosa. A continuación se muestran los gráficos de tres funciones que tienen un punto crítico en \(x = 0\), la segunda derivada de todas las funciones es cero en \(x = 0\) y, sin embargo, se exhiben las tres posibilidades.,
La primera es la gráfica de \(f\left( x \right) = {x^4}\). Este gráfico tiene un mínimo relativo en \(x = 0\).
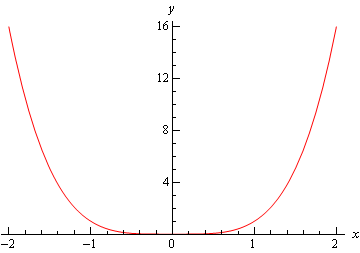
el Siguiente es el gráfico de \(f\left( x \right) = – {x^4}\), que tiene un máximo relativo en \(x = 0\).

finalmente, está el gráfico de \(f\left( x \right) = {x^3}\) y este gráfico no tenía ni un mínimo relativo ni un máximo relativo en \(x = 0\).
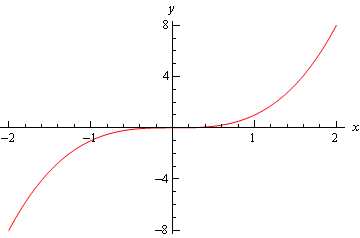
Así que, podemos ver que tenemos que tener cuidado si caemos en el tercer caso., Para aquellos momentos en los que entran en este caso tendremos que recurrir a otros métodos para clasificar el punto crítico. Esto generalmente se hace con la primera prueba de derivada.
retrocedamos y echemos un vistazo a los puntos críticos del primer ejemplo y utilicemos la segunda prueba derivada en ellos, si es posible.
vamos a trabajar un ejemplo más.















