Good Mood

Mobiler Hinweis anzeigen Alle Notizen anzeigen Ausblenden Aller Notizen

Abschnitt 4-6: Die Form eines Graphen, Teil II

Im vorherigen Abschnitt haben wir gesehen, wie wir die erste Ableitung einer Funktion verwenden können, um einige Informationen über den Graphen einer Funktion zu erhalten. In diesem Abschnitt werden wir uns die Informationen ansehen, die uns die zweite Ableitung einer Funktion über den Graphen einer Funktion geben kann.

Bevor wir dies tun, werden wir ein paar Definitionen aus dem Weg müssen. Das Hauptkonzept, das wir in diesem Abschnitt diskutieren werden, ist Konkavität. Konkavität ist am einfachsten mit einem Graphen zu sehen (wir geben die mathematische Definition in einem Bit).,

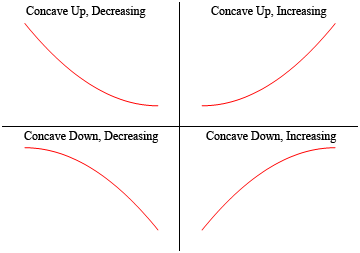
Eine Funktion ist also konkav, wenn sie sich“ öffnet „und die Funktion konkav, wenn sie sich“ öffnet“. Beachten Sie auch, dass Konkavität nichts mit Erhöhen oder Verringern zu tun hat. Eine Funktion kann konkav sein und entweder erhöhen oder verringern. In ähnlicher Weise kann eine Funktion nach unten konkav sein und entweder zunehmen oder abnehmen.

Es ist wahrscheinlich nicht der beste Weg, Konkavität zu definieren, indem man sagt, auf welche Weise sie „öffnet“, da dies eine etwas nebulöse Definition ist. Hier ist die mathematische Definition von Konkavität.,

Definition 1

Um zu zeigen, dass die obigen Diagramme tatsächlich eine oben beanspruchte Konkavität aufweisen, wird hier der Graph erneut angezeigt (etwas in die Luft gesprengt, um die Dinge klarer zu machen).

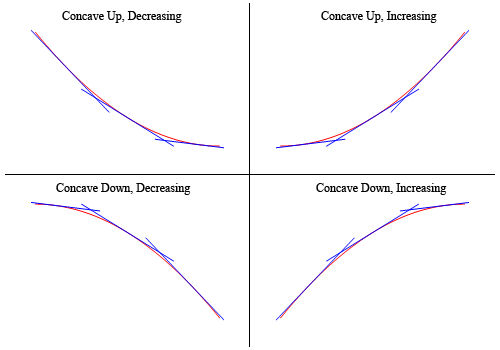
Wie Sie sehen, befinden sich in den beiden oberen Diagrammen alle skizzierten Tangenten unter dem Graphen der Funktion und diese sind konkav nach oben. In den unteren beiden Diagrammen befinden sich alle Tangentenlinien über dem Graphen der Funktion und diese sind konkav nach unten.,

Beachten Sie erneut, dass Konkavität und der zunehmende/abnehmende Aspekt der Funktion vollständig getrennt sind und nichts miteinander zu tun haben. Dies ist wichtig zu beachten, da die Schüler diese beiden häufig verwechseln und Informationen über eine verwenden, um Informationen über die andere zu erhalten.

Es gibt noch eine Definition, die wir brauchen, um aus dem Weg zu gehen.

Definition 2

Nachdem wir nun alle Konkavitätsdefinitionen aus dem Weg geräumt haben, müssen wir die zweite Ableitung in den Mix bringen. Wir haben schließlich diesen Abschnitt gestartet und gesagt, dass wir die zweite Ableitung verwenden würden, um Informationen über das Diagramm zu erhalten. Die folgende Tatsache bezieht die zweite Ableitung einer Funktion auf ihre Konkavität. Der Beweis dafür finden Sie im Abschnitt Beweise aus abgeleiteten Anwendungen des Kapitels Extras.

Fact

Also, was diese Tatsache uns sagt, ist, dass die Wendepunkte werden alle Punkte waren die zweite Ableitung Änderungen Zeichen., Wir haben im vorherigen Kapitel gesehen, dass eine Funktion die Zeichen ändern kann, wenn sie entweder Null ist oder nicht existiert. Beachten Sie, dass wir im vorherigen Abschnitt mit der ersten Ableitung gearbeitet haben, aber die Tatsache, dass eine Funktion möglicherweise Zeichen ändert, bei denen sie Null ist oder nicht existiert, hat nichts mit der ersten Ableitung zu tun. Es ist einfach eine Tatsache, die für alle Funktionen gilt, unabhängig davon, ob es sich um Derivate handelt oder nicht.,

Dies wiederum sagt uns, dass eine Liste möglicher Wendepunkte die Punkte sind, an denen die zweite Ableitung Null ist oder nicht existiert, da dies die einzigen Punkte sind, an denen die zweite Ableitung das Vorzeichen ändern könnte.

Achten Sie jedoch darauf, nicht davon auszugehen, dass der Punkt ein Wendepunkt ist, nur weil die zweite Ableitung Null ist oder nicht existiert. Wir werden erst dann wissen, dass es sich um einen Wendepunkt handelt, wenn wir die Konkavität auf beiden Seiten feststellen. Es wird nur ein Wendepunkt sein, wenn die Konkavität auf beiden Seiten des Punktes unterschiedlich ist.,

Nachdem wir nun über Konkavität Bescheid wissen, können wir diese Informationen sowie die zunehmenden/abnehmenden Informationen aus dem vorherigen Abschnitt verwenden, um eine ziemlich gute Vorstellung davon zu erhalten, wie ein Diagramm aussehen sollte. Schauen wir uns ein Beispiel dafür an.

Wir können das vorherige Beispiel verwenden, um eine andere Möglichkeit zu veranschaulichen, einige der kritischen Punkte einer Funktion als relative Maxima oder relative Minima zu klassifizieren.

Wie wir bald sehen werden, müssen wir mit \(x = 0\) sehr vorsichtig sein., In diesem Fall ist die zweite Ableitung Null, aber das bedeutet nicht, dass \(x = 0\) kein relatives Minimum oder Maximum ist. Wir werden einige Beispiele dafür in ein bisschen sehen,aber wir müssen einige andere Informationen zuerst kümmern.

Es ist auch hier wichtig zu beachten, dass alle kritischen Punkte in diesem Beispiel kritische Punkte waren, an denen die erste Ableitung Null war, und dies ist erforderlich, damit dies funktioniert. Wir werden diesen Test nicht an kritischen Punkten verwenden können, an denen die Ableitung nicht existiert.,

Hier ist der Test, mit dem einige der kritischen Punkte einer Funktion klassifiziert werden können. Der Beweis für diesen Test finden Sie im Abschnitt Beweise für abgeleitete Anwendungen im Kapitel Extras.

Zweiter Ableitungstest

Der dritte Teil des zweiten Ableitungstests ist wichtig zu beachten. Wenn die zweite Ableitung Null ist, kann der kritische Punkt alles sein. Unten sind die Graphen von drei Funktionen, die alle einen kritischen Punkt bei \(x = 0\) haben, die zweite Ableitung aller Funktionen ist Null bei \(x = 0\) und doch sind alle drei Möglichkeiten ausgestellt.,

Der erste ist der graph von \(f\left( x \right) = {x^4}\). Dieses Diagramm hat ein relatives Minimum bei \(x = 0\).

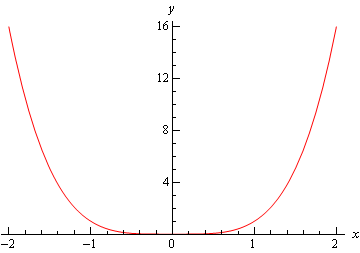
als Nächstes ist der graph von \(f\left( x \right) = – {x^4}\), die eine relative maximum bei \(x = 0\).

Schließlich gibt es das Diagramm von \(f\left( x \right) = {x^3}\) und dieses Diagramm hatte weder ein relatives Minimum noch ein relatives Maximum bei \(x = 0\).

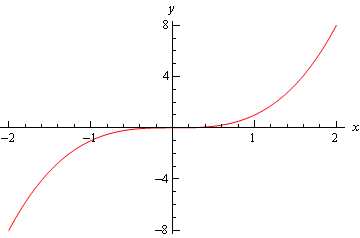
So können wir sehen, dass wir vorsichtig sein müssen, wenn wir in den dritten Fall fallen., Für die Zeiten, in denen wir in diesen Fall geraten, müssen wir auf andere Methoden zurückgreifen, um den kritischen Punkt zu klassifizieren. Dies geschieht normalerweise mit dem ersten Ableitungstest.

Gehen wir zurück und schauen uns die kritischen Punkte aus dem ersten Beispiel an und verwenden, wenn möglich, den zweiten Ableitungstest.

Lassen Sie uns ein weiteres Beispiel arbeiten.