Good Mood

stellen Sie sich das vor: Sie machen eine Präsentation Ihrer Ph. D.-Arbeit auf die Stabilität an einem der Seminare. Alles läuft reibungslos und schließlich ist Fragestunde! Und jemand aus heiterem Himmel fragt: „Was ist der Unterschied zwischen implizitem und explizitem Ansatz?”! Und da Sie statische Stabilität tun… haben Sie diese Begriffe noch nie gehört! Ja… das habe ich schon gemacht!, Jetzt bin ich ein bisschen klüger, also schauen wir uns die Unterschiede zwischen impliziter und expliziter Analyse genauer an

Implizite und explizite Analyse unterscheiden sich im Ansatz zur Zeitinkrementierung. In der impliziten Analyse muss jedes Zeitinkrement konvergieren, aber Sie können ziemlich lange Zeitinkremente festlegen. Explizit muss andererseits nicht jedes Inkrement konvergiert werden, aber damit die Lösung genau ist, müssen die Zeitschritte sehr klein sein.

Das klingt ziemlich einfach, oder?, Es sei denn, Sie beginnen, über Dinge wie „Welches sollte ich verwenden“ oder „Wie klein sollte das explizite Zeitintervall sein“ nachzudenken, und solche Dinge. Keine Sorge, ich habe dich abgedeckt!

Tauchen wir ein!

Dynamik vom Feinsten-implizit / explizit!

Sie verwenden implizite und explizite Löser, um dynamische Probleme zu lösen. Dies bedeutet, dass Sie dieses Zeug nicht kennen müssen, wenn Sie statische Analysen durchführen., Wenn Sie sich über den Unterschied zwischen statischer und dynamischer Analyse nicht sicher sind, lesen Sie bitte zuerst diesen Beitrag – dies erleichtert das Verständnis!

Dynamische Analyse in aller Kürze:

Dynamische Analyse löst Probleme, die Trägheit. Diese erscheinen, wenn sich die Dinge in Ihrem Modell schnell ändern (schnell angelegte Lasten, Stöße usw.). Ingenieure bezeichnen dies normalerweise als“nichtlineare Dynamik“.

Es sei darauf hingewiesen, dass Ingenieure häufig auch andere Analysen als“ dynamisch “ bezeichnen., Dinge wie Modalanalyse oder erzwungene Antwortanalyse, die sich mit Vibrationen befassen. Manchmal werden diese als „lineare Dynamik“ bezeichnet, aber es ist normalerweise eine gute Idee, sicherzustellen, was jemand meint, wenn er einen solchen Satz verwendet. Während „lineare dynamische“ Probleme wirklich interessant sind, werde ich diese hier nicht diskutieren. Sie können mehr über sie erfahren, indem Sie diesen Beitrag lesen!

Das erste, was ich wirklich betonen muss, ist, dass implizite und explizite Löser DIE GLEICHEN Probleme lösen!, Betrachten Sie es nicht als „verschiedene Löser“, sondern als zwei verschiedene Möglichkeiten, dasselbe Problem zu lösen.

In vielen Fällen können Sie sowohl implizite als auch explizite Solver, und sie werden das gleiche Ergebnis produzieren. Und ich denke, hier müssen wir anfangen!

Wie funktioniert die dynamische Analyse?

Beide Analysen lösen ein Problem, bei dem die Geschwindigkeit der Dinge wichtig ist. Dies bedeutet meistens, dass die Last sehr schnell aufgebracht wird. In solchen Fällen „iterieren“ Sie Ihre Ladung immer rechtzeitig., Grundsätzlich verwenden Sie die Zeit, um dem Solver mitzuteilen, „was passiert“ und wie sich die Last ändert.

Zunächst müssen Sie definieren, wie sich die Last zeitlich ändert. Sie tun dies normalerweise mit Diagrammen wie dem folgenden:

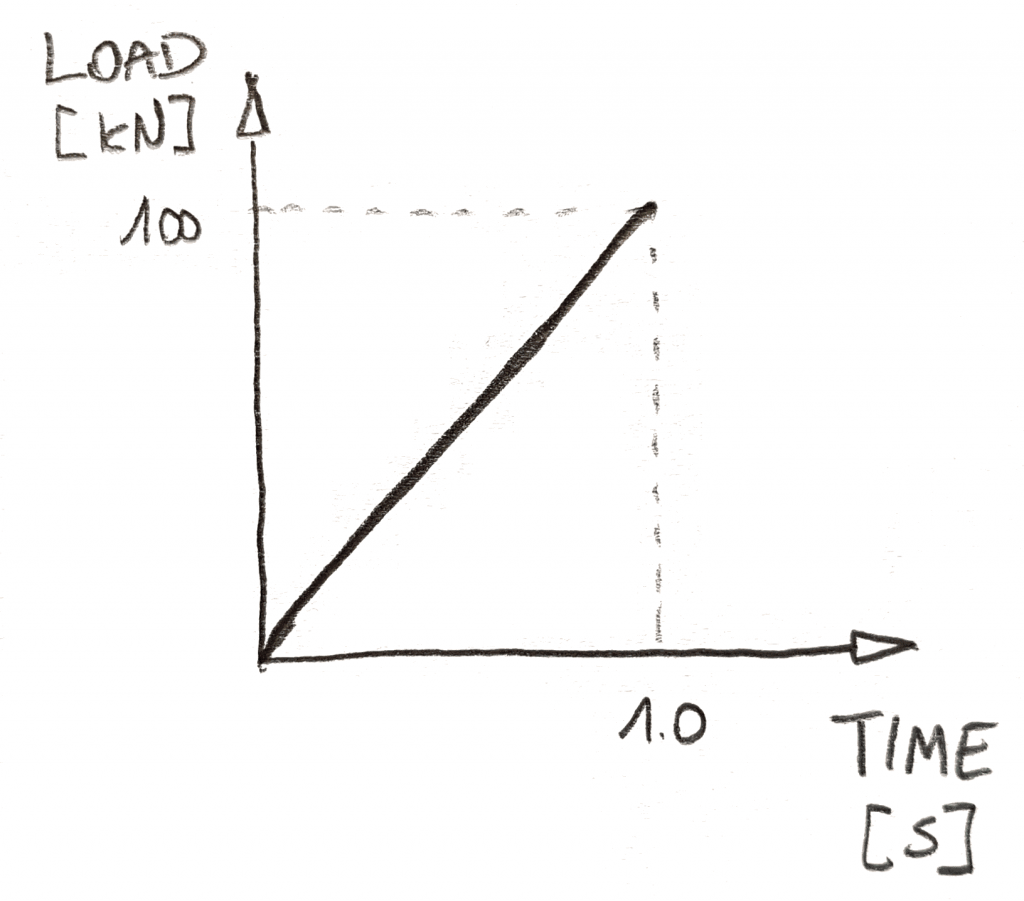
In der nichtlinearen dynamischen Analyse hat die Zeit 2 Rollen. Erstens können Sie dem Solver mitteilen, wann wie viel Last aufgebracht werden soll. Sie müssen einfach jede Last mit einem zeitabhängigen Diagramm implementieren. Zweitens … Zeit ist Zeit! Es sagt dem Löser, wie schnell die Dinge gehen!,

Stellen Sie sich vor, Sie möchten eine solche Ladesequenz haben:

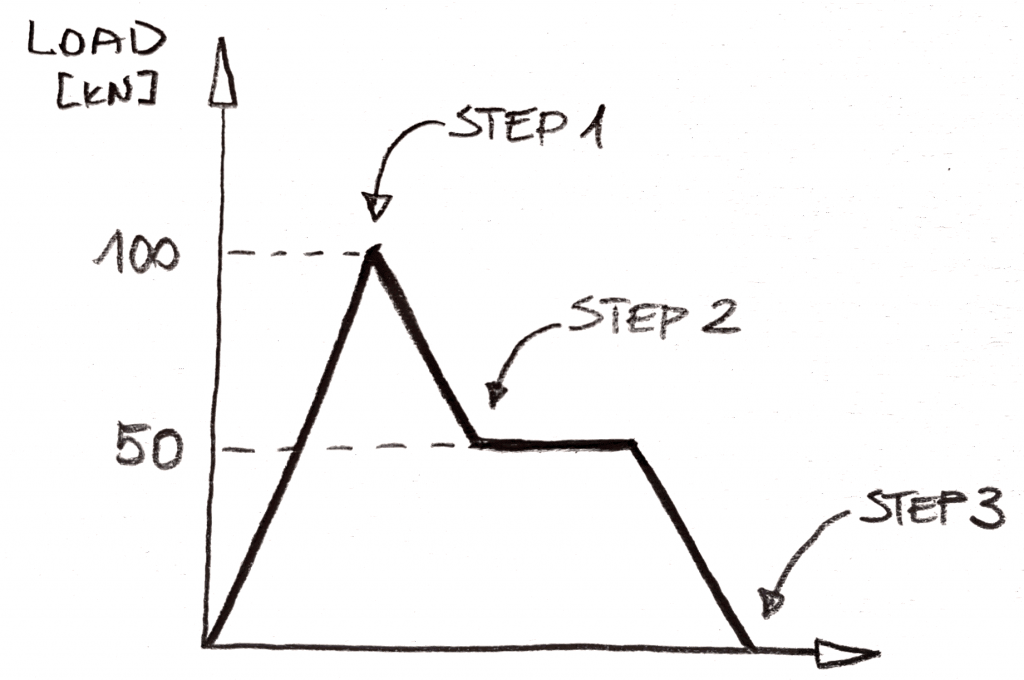
In static wäre dies eine 3″ steps “ – Analyse (diese werden in NX Nastran als subcases bezeichnet, aber ich denke, Abaqus hat tatsächlich „step“ als Namen verwendet, kann sich jedoch nicht sicher daran erinnern!). Die Idee wäre einfach, Sie müssen die 100kN der Last in Schritt 1 anwenden, dann 50kN der Last in Schritt 2 entfernen und 50kN in Schritt 3 entfernen. Es gibt keine Möglichkeit, das „Plateau“ der Last nach Schritt 2 in die Analyse aufzunehmen, und es wird weggelassen., Die Logik ist einfach: Keine Änderungen der Last = nichts ändert sich statisch!

Ladeschritte in statischen

Wenn das Problem sehr nichtlinear wäre, wäre die Last“inkrementiert“. Es ist selten in der Lage, „full load“ in nichtlineare Analyse bei „one go“anzuwenden! Normalerweise würde Solver dh 1kN jedes „Inkrement“anwenden. Dies bedeutet, dass nach 100 Schritten eine Volllast von Schritt 1 angewendet würde. Dies erleichtert es dem Löser, eine korrekte Antwort zu konvergieren.,

Als Benutzer können Sie definieren, wie große Inkremente solver verwenden soll. Es gibt auch einige Algorithmen, um die Lastinkrementierung während der Analyse zu ändern. Verschiedene Löser möchten, dass Sie dies auf unterschiedliche Weise festlegen. Normalerweise verwenden FEA-Pakete hierfür Lastmultiplikatoren. Dies bedeutet, dass Sie so etwas sagen können wie: „In jedem Inkrement zusätzliche 0,01 der gesamten Last anwenden“.

Geil… aber lasst uns an die Dynamik, sollen wir?, In der dynamischen Analyse können Sie die Lastverteilung wie oben mit einer solchen Lastdefinition erhalten:

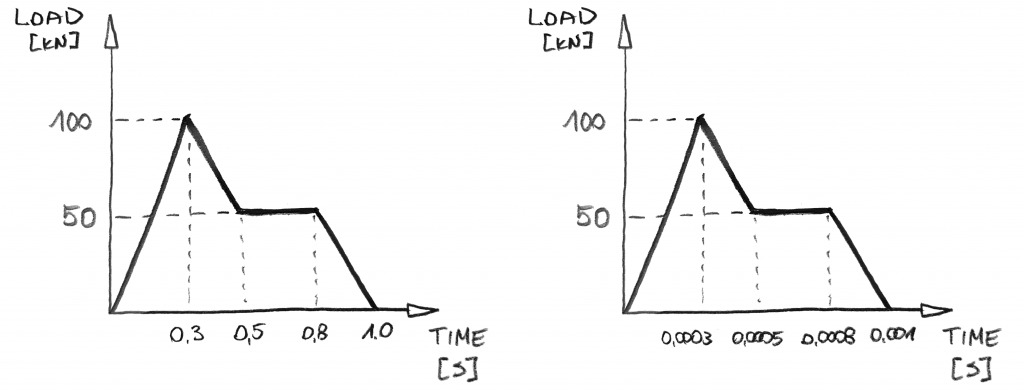
Sofort können Sie einige Dinge bemerken:

• Es gibt keine Schritte! Dies liegt daran, dass Sie in der dynamischen Analyse die Last nicht erhöhen. Sie werden die Zeit erhöhen! Und da die Zeit „ständig“ von Null auf den vorgeschriebenen Wert geht, können Sie sie in „einem Schritt“erhöhen.

• Zeit ist das Wesen! Wenn es um die Werte der Last geht, sind die obigen Diagramme gleich., Aber das ist nicht der gleiche dynamische Fall! Das Diagramm auf der rechten Seite wendet die Last 1000x schneller an! Dies ist nicht etwas, das Sie in der dynamischen Analyse einfach ignorieren können!

Wenn Sie ein dynamisches Problem lösen möchten, bitten Sie Ihren Löser im Allgemeinen, eine Sache zu tun. Sie bitten es, die Reihe von Zeitschritten zu berechnen, um zu sehen, was im Modell vor sich geht. In jedem dieser Inkremente nimmt die Zeit leicht zu. Dies ändert natürlich auch die Last im Modell. Aus diesem Grund benötigen Sie ein zeitabhängiges Diagramm zum Laden., Der Löser „weiß“ also, welche Last zu welchem Zeitpunkt angewendet werden soll. In diesem Maße funktioniert es genauso wie die Lastinkrementierung in der statischen Analyse. Der Bonus ist, dass, da Sie die Zeit erhöhen, Trägheitseffekte berücksichtigt werden können, wenn die Dinge schnell genug geschehen.

In diesem Ausmaß machen sowohl implizite als auch explizite Analysen mehr oder weniger dasselbe. Sie teilen die „Analysezeit“ in kleine Inkremente auf und analysieren dann, was in Ihrem Modell nacheinander vor sich geht. Aber hier enden die ähnlichkeiten!, Sie sehen, es gibt verschiedene Ansätze zur Zeitinkrementierung, die Sie möglicherweise haben!

Implizit vs explizit-Wenn die Zeit wirklich zählt!

Sie haben gerade erfahren, dass Sie zur Berechnung des nichtlinearen dynamischen Problems die“Analysezeit“ schrittweise erhöhen müssen. Wie bereits erwähnt, kann dies auf zwei Arten erfolgen.

Ich werde mit dem impliziten Ansatz beginnen. Ich denke, es ist einfacher zu verstehen, da es in der nichtlinearen statischen Analyse mehr oder weniger genauso funktioniert wie die Lastinkrementierung!,

Wie implizite Analyse funktioniert:

Zuallererst scheint implizit eine“ grundlegendere “ Lösung zu sein. Im Wesentlichen funktioniert es genau so, wie Sie es sich vorstellen würden!

• Erstens wird bei jedem Inkrement das“ globale Gleichgewicht “ im Modell hergestellt. Dies bedeutet, dass jedes Inkrement konvergieren muss (dies geschieht in Iterationen).

• Nachdem das globale Gleichgewicht in Ordnung ist, berechnet solver alle lokalen Finite-Elemente-Variablen (Spannungen usw.) für dieses Inkrement.,

• Vorteile: Da das globale Gleichgewicht bei jedem Zeitschritt überprüft wird, können diese Inkremente GROß sein!
• Nachteile: Jedes Mal wird das Inkrement langsam berechnet, da Iterationen benötigt werden, um zum globalen Gleichgewicht zu gelangen.

Wenn Sie mit der nichtlinearen statischen Analyse vertraut sind, fühlen Sie sich mit dem impliziten Löser“ zu Hause“. Als Benutzer können Sie normalerweise sagen, wie groß die Zeitschritte sind, die Sie haben möchten. Dies ist ein großer Vorteil… der leicht zu übersehen ist., Weil Explicit Solver keine solche Möglichkeit bietet!

Schauen wir uns als nächstes die explizite Inkrementierung an!

Wie explizite Analyse funktioniert:

Dieser ist funky. Es funktioniert so, dass Sie nicht jeden Schritt konvergieren müssen! Es gibt keine Konvergenzkriterien zu überprüfen und… keine Iterationen! Anstatt das „globale Gleichgewicht“ zu überprüfen, geht der Löser davon aus, dass das Gleichgewicht „einfach existiert“. Dies bedeutet, dass der Solver direkt in die Berechnung lokaler Finite-Elemente-Variablen eingeht!, Da eine solche Prozedur nur einen Schritt hat:

• Berechnen Sie alle lokalen Finite-Elemente-Variablen für ein bestimmtes Inkrement und wechseln Sie zum nächsten!

• Vorteile: Jede Einheit berechnet, extrem schnell!
• Nachteile: Damit dies funktioniert, muss der Zeitschritt EXTREM klein sein. Andernfalls ist es unmöglich, dieses Gleichgewicht aufrechtzuerhalten, von dem angenommen wird, dass es „einfach existiert“. Um dies zu erreichen, Benutzer haben keine direkte Kontrolle darüber, wie Groß-Zeit-Schritten expliziten Löser nehmen., Solver selbst berechnet, wie kleine Zeitschritte noch in Ordnung sind. Und diese akzeptablen Zeitschritte sind SUPER KLEIN! Deshalb sollten explizite Probleme Bruchteile einer Sekunde dauern! Wenn sie Sekunden dauern würden… würden Sie Millionen von Schritten benötigen!

Um es schnell zusammenzufassen: Sowohl implizite als auch explizite Löser lösen dasselbe. Der einzige Unterschied ist, wie diese Methoden die Zeit erhöhen.

Technisch gesehen sollten beide für alle Fälle das gleiche Ergebnis erzielen., Schließlich können Sie dasselbe Problem mit beiden Ansätzen analysieren. Offensichtlich kann die Antwort nicht von der Methode abhängen, mit der das Problem gelöst wird! Aber natürlich werden Sie nur einen der Ansätze für Ihr nächstes Problem auswählen, also welchen? Lass es uns herausfinden!

Was ist Besser für Sie: Implizit oder Explizit?

Wir haben bereits vereinbart, dass Sie sowohl implizite als auch explizite Löser verwenden können, um die gleiche Art von Problemen zu lösen. Der einzige Unterschied besteht in der Annäherung an die Zeitinkrementierung. Aber es ist keine triviale Sache!, Wenn der Unterschied gering wäre, würde sich niemand darum kümmern, beides zu implementieren! Schauen wir uns also an, wie diese zeitliche Inkrementierung die Dinge beeinflusst!

Sowohl implizite als auch explizite Löser haben einige Bereiche, in denen sie glänzen. Und es gibt eine Überlappung in ihrer Verwendung:

• Mit der impliziten Analyse können Sie auswählen, wie groß das Zeitinkrement sein soll! Dieses Inkrement wird einige Zeit in Anspruch nehmen, da es zuerst für das globale Gleichgewicht iterieren muss. Aber Sie können es für Ihre Analyse „einigermaßen groß“ machen.,

• Explicit Zeit-Schritten berechnen Sie die wirklich schnell! Einfach weil sie nicht für das globale Gleichgewicht iterieren… aber das zeitliche Inkrement dort ist nicht Ihre Wahl! Solver geht einfach davon aus, dass das „akzeptable“ Zeitinkrement „X“ ist und geht damit einher. Beachten Sie, dass dieses “ X “ leicht so etwas wie 5e-7s sein kann… Das ist super klein! Um ein Problem zu lösen, das über 1s auftritt, benötigen Sie 2 000 000 Inkremente!

• Und das ist es! Die Geschwindigkeit der Berechnung ist genau der Unterschied zwischen implizit und explizit., Natürlich hängt die Größe des Schritts von Ihrem Modell ab und die Rechenzeiten hängen von Ihrer Hardware ab. Es gibt jedoch einfache Beobachtungen, die wir leicht machen können:

Verwenden Sie implizit für „langsame Analyse“!

Wenn das, was Sie berechnen, über mehrere Sekunden passiert… macht es keinen Sinn, einen expliziten Löser zu verwenden. Es wird ewig dauern, die Millionen von Zeitschritten zu durchforsten, die für die Berechnung benötigt werden!, Legen Sie stattdessen einen „vernünftigen“ Zeitschritt für die implizite Analyse fest (sagen wir 100 gleiche Zeitschritte für Ihre Analyse). Sicher, jedes dieser impliziten Zeitinkremente berechnet viel länger als ein einzelnes explizites Inkrement. Aber nicht länger als Hunderttausende von ihnen!

Verwenden Sie explizit für die „schnelle Analyse“!

Das ist offensichtlich, oder? Wenn das, was Sie berechnen, im Bruchteil einer Sekunde passiert, ist Ihr Freund., In einer impliziten Analyse wäre Ihr Zeitinkrement sehr klein… vielleicht sogar so klein wie das Inkrement in einer expliziten Analyse. In einem solchen Fall läuft die explizite Analyse VIEL schneller, da keine Iterationen des „globalen Gleichgewichts“ erforderlich sind. Die implizite Analyse erfordert diese Iterationen (unabhängig vom Zeitschritt!).

Dazwischen Sachen!

Natürlich gibt es Probleme, die in der Mitte auftreten (wie ein Aufprall mit 5m/s Geschwindigkeit)., Normalerweise können Sie ein solches Problem mit beiden Lösern lösen, aber es kann ärgerlich sein.

Ich hoffe, dass dies Ihnen hilft, einen geeigneten Ansatz für Ihre dynamischen Probleme auszuwählen. Am Ende ist die Erfahrung natürlich der beste Leitfaden! Wenn Sie Zweifel haben, führen Sie einige Ihrer typischen Probleme sowohl implizit als auch explizit aus. Auf diese Weise können Sie die Ergebnisse vergleichen (sie sollten gleich sein). Aber was noch wichtiger ist, Sie können die Rechenzeiten vergleichen! Dies gibt Ihnen die Möglichkeit zu überprüfen, was ist ein besserer Ansatz für Sie!,

Wie explizit errät Zeit Schrittgröße?

Nun, es ist alles schön und dandy so weit, aber ich denke, es wäre schön, ein großes Problem anzugehen. Und das ist… wenn Sie den Zeitschritt in Ihrer expliziten Analyse nicht auswählen… wer dann?

Die mathematische Erklärung würde eine Diskussion über die maximale Eigenfrequenz erfordern. Dies liegt daran, dass das maximale“ noch akzeptable “ Zeitinkrement umgekehrt proportional zur maximalen Eigenfrequenz ist. Solche Berechnungen können natürlich durchgeführt werden., Die Ergebnisse hängen vom Mesh des Modells ab (wie viele Elemente gibt es usw.). Aber wir werden nicht dorthin gehen, und es gibt zwei Gründe, warum: Erstens mag ich Mathe nicht (!). Zweitens machen es die Löser am Ende nicht so, obwohl dies der „richtige Weg“ist.

Der Solver kann natürlich die maximale Eigenfrequenz berechnen, dies dauert jedoch einige Zeit. Und da es in jedem expliziten Zeitschritt getan werden müsste (es kann viele davon geben!)… Huch!, Glücklicherweise gibt es eine Möglichkeit, diesen Wert gut zu schätzen, indem jedes endliche Element im System separat analysiert wird! Die physikalische Interpretation dieser Schätzung (die üblicherweise in Lösern verwendet wird) lautet:

Maximales Zeitinkrement in expliziter Analyse:

Das Zeitinkrement in expliziter Analyse ist sehr kurz. Es ist die Zeit, in der eine elastische Welle (dh Aufprallwelle) durch ein einzelnes endliches Element Ihres Modells wandern kann. Dies wird natürlich für alle endlichen Elemente in Ihrem Modell überprüft und die kleinste Zeit ausgewählt.,

Wie Sie sehen, gibt es 2 Komponenten für die explizite Zeitkomponente:

• Elastische Wellengeschwindigkeit (auch bekannt als Schallgeschwindigkeit in Ihrem Material)! Dies hängt nur von dem Material ab, das Sie in Ihrem Modell haben (und es ist natürlich für verschiedene Materialien unterschiedlich!). Sie benötigen den jungen Modul E, die Materialdichte und die Poisson-Ration (bei 2D-und 3D-Problemen). Es ist einfach, Tabellen zu finden, die elastische Wellengeschwindigkeiten in verschiedenen Materialien auflisten. Nur als referenz in stahl, dies ist um 5200 mt/s (viele metalle sind um 4500-5500 mt / s).,

• Elementgröße (und Qualität)! Sie haben die Wellengeschwindigkeit, aber es ist nicht genug! Um die Zeit zu kennen, die es benötigt, um durch das Element zu reisen, müssen Sie das Element „Länge“kennen. Während dies in 1D-Elementen super einfach ist (sie haben einfach Länge), wird es in 2D und 3D schwierig. Diese Länge ist nicht „einfach“ die kürzeste der Elementkanten, da Elemente eine ziemlich schlechte Geometrie haben können. Es gibt Dinge, die Solver tut, um dies zu berechnen. In 2D könnte es sich um einen Elementbereich handeln, der durch die maximale Kantenlänge geteilt wird., In 3D kann das bedeuten, dass das Volumen des Elements durch den maximalen Seitenbereich geteilt wird. Aus diesem Grund ist nicht nur die Elementgröße, sondern auch die Elementqualität bei der expliziten Analyse so wichtig! Immerhin … alles, was Sie brauchen, ist ein armes Element, um Ihre Rechenzeit wirklich zu verletzen!

Ich habe irgendwo gelesen, dass Löser häufig“ Sicherheitsfaktoren „verwenden, während das Obige die“ genaue “ Lösung ist. Wenn Sie eine höhere Zeit-Inkrement als die elastische Welle „Geschwindigkeitsbegrenzung“ mathematische Fehler auftreten. Da Schätzungen verwendet werden, reduzieren Löser oft den Zeitschritt „nur für den Fall“., Normalerweise liegt der Reduktionsfaktor bei etwa 0,9, aber dies kann natürlich von Löser zu Löser variieren.

Massenskalierung!

am Ende möchte ich erwähnen, etwas zu schnell.

Ihnen ist höchstwahrscheinlich aufgefallen, dass der Zeitschritt in explicit nur vom Netz, dem jungen Modul und der Dichte abhängt. Das Reduzieren des Moduls ist natürlich nicht ideal, und Sie benötigen oft ein kleines Netz, um Details zu analysieren. Bei „niedrigen dynamischen“ Problemen können Sie jedoch versuchen, die explizite Zeit schrittweise zu erhöhen, indem Sie die Materialdichte erhöhen.,

Dies wird als“Massenskalierung“ bezeichnet. FEA-Pakete bieten sogar Lösungen an, bei denen die Dichte nur in den Elementen erhöht wird, die über die zeitliche Erhöhung „entscheiden“. Dies bedeutet, dass manchmal nur kleine Teile Ihres Modells schwerer werden! In einigen Analysen können Sie mit der Erhöhung der Masse Ihres Modells „davonkommen“. Wenn dies der Fall ist, kann dies eine Lösung für Sie sein. Seien Sie sich bewusst, dass dies das Verhalten Ihres Modells ändert! Wenn hohe Beschleunigungen beteiligt sind, ist es am besten vorsichtig zu sein!

Zusammenfassung

Nice!, Sie haben hier, danke fürs Lesen! Lass uns das einpacken, damit es leichter zu merken ist!

• Dynamische Analyse umfasst die Zeit! Wenn Sie Lasten anwenden, müssen diese in einer Zeitfunktion definiert werden. Oft ist dies eine lineare Beziehung. Dies ändert sich jedoch nicht, dass die Zeit, in der Last angewendet wird, eine bedeutende Rolle spielt (besonders wenn diese Zeit kurz ist!).

• 2 Aromen von dynamischen Analyse! Sie können die „echten“ dynamischen Probleme mit impliziten und expliziten Algorithmen lösen. Beide sind in Ordnung, und kein einziger von ihnen ist „besser“., Aber ich sollte sagen, dass der explizite Löser Teil weniger FEA-Pakete ist. Da nicht jedes FEA-Paket sogar eines hat, wird der explizite Löser als „fortgeschrittenere“ Sache angesehen.

• Der implizite Löser ist wirklich gut, wenn Dinge in Ihrer Analyse relativ langsam passieren. Nehmen wir an, die Analyse ist länger als 1s, ohne dass während dieser Zeit abrupte Dinge passieren. Der Vorteil ist, dass Sie auswählen können, wie groß die gewünschte Zeiterhöhung ist. Selbst wenn die Berechnung des einzelnen Inkrements länger dauert, gibt es viel weniger davon!,

• Der explizite Löser eignet sich hervorragend für schnell geschehene Dinge (sagen wir schneller als 0,1 s). Sie können hier nicht das Zeitinkrement auswählen – Solver stellt es automatisch ein. Während sie normalerweise super klein sind, berechnen sie zumindest viel schneller als die „impliziten“. Explicit Solver berechnet, wie groß das Zeitinkrement sein sollte. Dies hängt von der Schallgeschwindigkeit in Ihrem Material, der minimalen Finite-Elemente-Größe (und der Elementqualität!). In einigen Fällen können Sie die Dichte ändern (auch automatisch nur in „Entscheidungselementen“!), um dieses Zeit-Inkrement anzupassen., Dies funktioniert, da die Schallgeschwindigkeit in Ihrem Material von seiner Dichte abhängt! Dies wird als „Massenskalierung“bezeichnet.