Biografi – Der var Pascal

Blaise Pascal (1623-1662)
Franskmanden Blaise Pascal, var en fremtrædende 17 Århundrede, videnskabsmand, filosof og matematiker. Ligesom så mange store matematikere, han var et vidunderbarn og forfulgt mange forskellige veje af intellektuelle bestræbelser hele sit liv., Meget af hans tidlige arbejde var inden for naturvidenskab og anvendt videnskab, og han har en fysisk lov opkaldt efter ham (at “tryk, der udøves overalt i en begrænset væske, overføres lige og uformindsket i alle retninger gennem væsken”) såvel som den internationale enhed til måling af tryk. I filosofi er Pascals ‘ indsats hans pragmatiske tilgang til at tro på Gud med den begrundelse, at det er en bedre “indsats” end ikke at gøre.
men Pascal var også en matematiker af den første orden., I en alder af seksten, skrev han en betydelig afhandling om emnet Projektiv geometri, kendt som Pascal ‘ s sætning, hvori det hedder, at hvis en sekskant er indskrevet i en cirkel, så de tre skæringspunkter af modsatte sider ligger på en enkelt linje, kaldet Pascal linje. Som ung mand byggede han en funktionel beregningsmaskine, der kunne udføre tilføjelser og subtraktioner for at hjælpe sin far med sine skatteberegninger.,
Pascal ‘ s Trekant
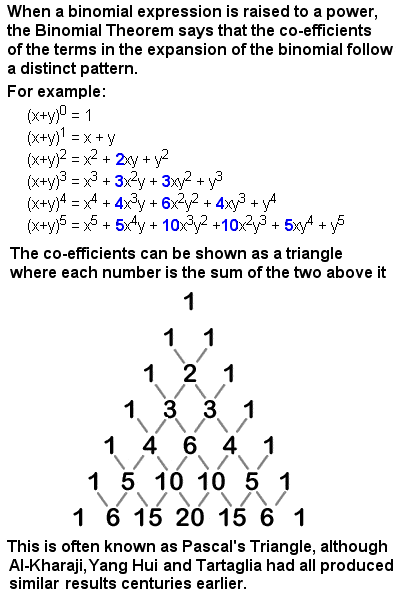
tabellen af binomial koefficienter, der er kendt som Pascal ‘s Trekant
Han er dog bedst kendt for Pascal’ s Trekant, en praktisk tabelform præsentation af binomial-koefficienter, hvor hvert tal er summen af de to tal direkte oven over det. En binomial er en simpel type algebraisk udtryk, som kun har to udtryk, der kun drives af addition, subtraktion, multiplikation og positive hele tal eksponenter, såsom (y + y)2., De co-efficienter, der produceres, når en binomial udvides, danner en symmetrisk trekant (se billedet til højre).
Pascal var langt fra den første til at studere denne trekant. Den persiske matematiker Al-Karaji havde produceret noget meget lignende allerede i det 10. århundrede, og trekanten kaldes Yang Huis trekant i Kina efter det 13.århundrede kinesiske matematiker, og Tartaglia ‘ s trekant i Italien efter den eponyme 16. århundrede italiensk., Men Pascal gjorde bidrage med en elegant bevis ved at definere tallene ved rekursion, og han har også opdaget mange nyttige og interessante mønstre blandt de rækker, kolonner og diagonaler af den vifte af numre. For eksempel ser man alene på diagonalerne, efter den udvendige” hud “af 1’ erne, den næste diagonale (1, 2, 3, 4, 5,…) er de naturlige tal i rækkefølge. Den næste diagonal inden for det (1, 3, 6, 10, 15,…) er de trekantede tal i rækkefølge. Den næste (1, 4, 10, 20, 35,…) er de pyramidale trekantede tal osv., Det er også muligt at finde primtal, Fibonacci tal, catalanske tal, og mange andre serier, og endda at finde fraktale mønstre i det.
Pascal gjorde også det konceptuelle Spring til at bruge trekanten til at hjælpe med at løse problemer i sandsynlighedsteorien. I virkeligheden, blev det gennem hans samarbejde og korrespondance med sin franske moderne Pierre de Fermat og Hollænderen Christiaan Huygens om emnet, at den matematiske teori om sandsynligheden for, blev født., Før Pascal var der ingen egentlig sandsynlighedsteori-uanset Gerolamo Cardanos tidlige udstilling i det 16.århundrede – blot en forståelse (af slags) af, hvordan man beregner “chancer” i terninger og kortspil ved at tælle lige så sandsynlige resultater. Nogle tilsyneladende helt elementære problemer i Sandsynlighed havde undgået nogle af de bedste matematikere, eller givet anledning til forkerte løsninger.,
Den faldt til Pascal (med Fermat ‘s hjælp) til at samle de forskellige tråde af forudgående viden (herunder Cardano’ s tidlige arbejde), og indføre helt nye matematiske metoder til løsning af problemer, der hidtil havde modstået løsning., To uforsonlige problemer, som Pascal og Fermat anvendes sig selv var Gambler Ruin (bestemmelse af chancer for at vinde for hver af de to mænd spille en særlig terninger spil med særlige regler), og Problemet i at afgøre, hvordan et spil er gevinsterne skal fordeles mellem de to lige så dygtige spillere, hvis spillet blev afbrudt). Hans arbejde med problemet med punkter i særdeleshed, selv om ikke-offentliggjorte på det tidspunkt, var meget indflydelsesrig i udfoldelsen af nye område.,
Problemet Point

Fermat og Pascal ‘ s løsning på Problemet med Points
Problemet med Point i sin simpleste kan illustreres ved et simpelt spil “vinderen tager alle”, som indebærer at smide en mønt. Den første af de to spillere (Fermat og Pascal) for at opnå ti point eller vinder er at modtage en pot på 100 francs. Men hvis spillet afbrydes på det punkt, hvor Fermat, siger, vinder 8 point til 7, Hvordan er 100 franc pot til delt?, Fermat påstod, at, som han behøvede kun to point for at vinde spillet, og Pascal havde brug for tre, spillet ville have været over efter yderligere fire kaster af mønten (fordi, hvis Pascal ikke fik den nødvendige 3 point for din sejr over de fire kaster, så Fermat, som har opnået de nødvendige 2 point for sin sejr, og vice versa. Fermat opregnede derefter udtømmende de mulige resultater af de fire kast og konkluderede, at han ville vinde i 11 ud af de 16 mulige resultater, så han foreslog, at 100 francs blev delt 11⁄16 (0.6875) til ham og 5 16 16 (0.3125) til Pascal.,
Pascal derefter kiggede efter en måde at generalisere problemet, der ville undgå den kedelige liste af muligheder, og indså, at han kunne bruge rækker fra hans trekant af koefficienter til at generere tal, uanset hvor mange kaster af mønten tilbage. Da Fermat havde brug for 2 flere point for at vinde spillet, og Pascal havde brug for 3, gik han til den femte (2 + 3) række i trekanten, dvs. 1, 4, 6, 4, 1., De første 3 udtryk tilføjet sammen (1 + 4 + 6 = 11) repræsenterede de resultater, hvor Fermat ville vinde, og de sidste to udtryk (4 + 1 = 5) de resultater, hvor Pascal ville vinde, ud af det samlede antal resultater repræsenteret af summen af hele rækken (1 + 4 + 6 +4 +1 = 16).
Pascal og Fermat havde forstået gennem deres korrespondance et meget vigtigt begreb, men måske intuitivt for os i dag, var alle, men revolutionerende i 1654., Dette var ideen om lige så sandsynlige resultater, at sandsynligheden for noget forekommende kunne beregnes ved at opregne antallet af lige så sandsynlige måder, det kunne forekomme, og dividere dette med det samlede antal mulige resultater af den givne situation. Dette tillod brugen af fraktioner og forhold i beregningen af sandsynligheden for begivenheder og driften af multiplikation og tilføjelse på disse brøkdele sandsynligheder., For eksempel, sandsynligheden for at smide en 6 på en dør to gange er 1⁄6 x 1⁄6 = 1⁄36 (“og” fungerer som multiplikation); sandsynligheden for at kaste enten en 3 eller 6 er 1⁄6 + 1⁄6 = 1⁄3 (“eller” fungerer som supplement).senere i livet identificerede Pascal og hans søster Jac .ueline sig stærkt med Jansenismens ekstreme katolske religiøse bevægelse. Efter sin fars død og en” mystisk oplevelse “i slutningen af 1654 havde han sin” anden konvertering ” og opgav sit videnskabelige arbejde fuldstændigt og dedikerede sig til filosofi og teologi., Hans to mest berømte værker,” Lettres provinciales “og” Penseses”, stammer fra denne periode, sidstnævnte forlod ufuldstændige ved hans død i 1662. De forbliver Pascal ‘ s bedst kendte arv, og han er som regel huskes i dag som en af de vigtigste forfattere i den franske Klassiske Periode og en af de største mestre af den franske prosa, meget mere end for hans bidrag til matematik.,
| << Back to Fermat | Forward to Newton >> |















