Good Mood

Vis Mobile Varsel Vis Alle Noter Skjule Alle Noter

Afsnit 4-6 : Formen på en Graf, Del II

I det foregående afsnit så vi, hvordan vi kan bruge den første afledede af en funktion til at få nogle oplysninger om grafen for en funktion. I dette afsnit skal vi se på de oplysninger, som det andet derivat af en funktion kan give os en om grafen for en funktion.

før vi gør dette, har vi brug for et par definitioner ud af vejen. Det vigtigste koncept, som vi vil diskutere i dette afsnit, er konkavitet. Konkavitet er nemmest at se med en graf (vi giver den matematiske definition lidt).,

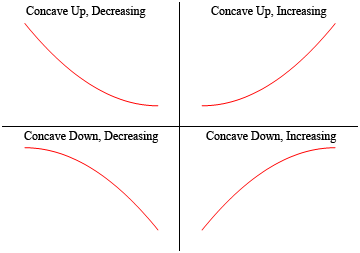
så en funktion er konkav op, hvis den “åbner” op, og funktionen er konkav ned, hvis den “åbner” ned. Bemærk også, at konkavitet ikke har noget at gøre med stigende eller faldende. En funktion kan være konkave op og enten stigende eller faldende. Tilsvarende kan en funktion være konkav ned og enten stigende eller faldende.

det er nok ikke den bedste måde at definere konkavitet ved at sige, hvilken vej det “åbner”, da dette er en noget nebulous definition. Her er den matematiske definition af konkavitet.,

Definition 1

for at vise, at graferne ovenfor faktisk har konkavitet hævdet ovenfor her, er grafen igen (sprængt lidt for at gøre tingene klarere).

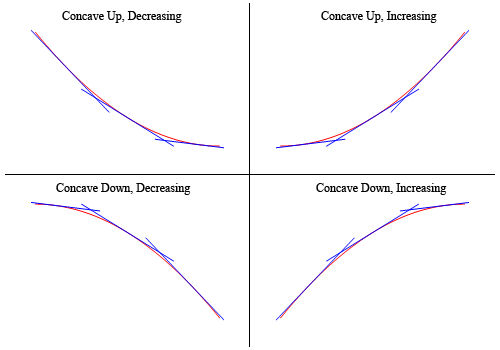
Så, som du kan se, i de to øverste grafer alle af tangenten linjer skitseret i er alle under grafen for funktionen og disse er konkave op. I de to nederste grafer er alle tangentlinjerne over grafen for funktionen, og disse er konkave ned.,

igen skal du bemærke, at konkavitet og det stigende / faldende aspekt af funktionen er helt adskilt og ikke har noget at gøre med hinanden. Dette er vigtigt at bemærke, fordi studerende ofte blander disse to sammen og bruger oplysninger om den ene til at få oplysninger om den anden.

Der er endnu en definition, som vi har brug for at komme ud af vejen.

Definition 2

nu hvor vi har alle konkavitetsdefinitionerne ud af den måde, vi har brug for at bringe det andet derivat ind i blandingen. Vi startede trods alt dette afsnit og sagde, at vi skulle bruge det andet derivat til at få oplysninger om grafen. Følgende kendsgerning relaterer det andet derivat af en funktion til dets konkavitet. Beviset for denne kendsgerning findes i afsnittet Proofs From Derivative Applications i kapitlet ekstra.

faktum

Så hvad denne kendsgerning fortæller os er, at bøjningspunkterne vil være alle punkterne var det andet derivatændringstegn., Vi så i det forrige kapitel, at en funktion kan ændre tegn, hvis den enten er nul eller ikke findes. Bemærk, at vi arbejdede med det første derivat i det foregående afsnit, men det faktum, at en funktion muligvis ændrer tegn, hvor den er nul eller ikke findes, har intet at gøre med det første derivat. Det er simpelthen en kendsgerning, der gælder for alle funktioner, uanset om de er derivater eller ej.,dette fortæller os igen, at en liste over mulige bøjningspunkter vil være de punkter, hvor det andet derivat er nul eller ikke findes, da disse er de eneste punkter, hvor det andet derivat kan ændre tegn.vær dog forsigtig med ikke at antage, at bare fordi det andet derivat er nul eller ikke eksisterer, vil punktet være et bøjningspunkt. Vi ved kun, at det er et bøjningspunkt, når vi først har bestemt konkaviteten på begge sider af det. Det vil kun være et bøjningspunkt, hvis konkaviteten er forskellig på begge sider af punktet.,

nu hvor vi ved om konkavitet, kan vi bruge disse oplysninger såvel som de stigende / faldende oplysninger fra det foregående afsnit for at få en ret god id.om, hvordan en graf skal se ud. Lad os se på et eksempel på det.

Vi kan bruge det foregående eksempel til at illustrere en anden måde at klassificere nogle af de kritiske punkter i en funktion som relative maksimum eller relative minimum.

som vi ser lidt, bliver vi nødt til at være meget forsigtige med \(\=0\)., I dette tilfælde er det andet derivat nul, men det betyder faktisk ikke, at \(0 = 0\) ikke er et relativt minimum eller maksimum. Vi vil se nogle eksempler på dette i en smule, men vi har brug for at få nogle andre oplysninger taget sig af først.

det er også vigtigt at bemærke her, at alle de kritiske punkter i dette eksempel var kritiske punkter, hvor det første derivat var nul, og dette er nødvendigt for at dette kan fungere. Vi vil ikke være i stand til at bruge denne test på kritiske punkter, hvor derivatet ikke findes.,

Her er den test, der kan bruges til at klassificere nogle af de kritiske punkter i en funktion. Beviset for denne test findes i afsnittet Proofs of Derivative Applications i kapitlet ekstra.

anden Derivattest

den tredje del af den anden derivattest er vigtig at lægge mærke til. Hvis det andet derivat er nul, kan det kritiske punkt være noget. Nedenfor er graferne for tre funktioner, som alle har et kritisk punkt på \(0 = 0\), det andet derivat af alle funktionerne er nul ved \(0 = 0\), og alligevel vises alle tre muligheder.,

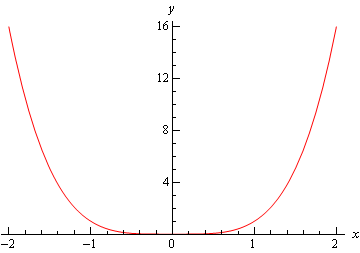
den første er grafen for \(f\venstre (\\højre) = {^^4}\). Denne graf har et relativt minimum ved \(0 = 0\).

næste er grafen for \(f\venstre (\\højre) = – {^^4}\), som har et relativt maksimum ved\(. = 0\).

endelig er der grafen for \(f\venstre( left \højre) = {^^3}\), og denne graf havde hverken et relativt minimum eller et relativt maksimum ved \(. = 0\).

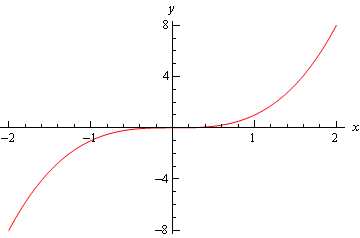
så vi kan se, at vi skal være forsigtige, hvis vi falder ind i det tredje tilfælde., For de tidspunkter, hvor vi falder ind i denne sag, bliver vi nødt til at ty til andre metoder til at klassificere det kritiske punkt. Dette gøres normalt med den første derivattest.

lad os gå tilbage og se på de kritiske punkter fra det første eksempel og bruge den anden Derivattest på dem, hvis det er muligt.

lad os arbejde endnu et eksempel.