Good Mood

Billede dette: Du skal lave en præsentation af din Ph. D.-afhandling om stabilitet på et af seminarerne. Alt går glat, og endelig er det spørgetid! Og nogen ud af det blå spørger: “Hvad er forskellen mellem implicit og eksplicit tilgang?”! Og da du gør statisk stabilitet … du aldrig selv hørt disse vilkår! Ja, det har jeg gjort!, Nu er jeg lidt klogere, så lad os se nærmere på forskellene mellem Implicit og eksplicit analyse

Implicit og eksplicit analyse adskiller sig i tilgangen til tidsforøgelse. I Implicit analyse hver gang tilvækst skal konvergere, men du kan indstille temmelig lang tid intervaller. Eksplicit på den anden side behøver ikke at konvergere hver tilvækst, men for at løsningen skal være nøjagtige tidsintervaller skal være super små.

dette lyder ret simpelt, ikke?, Medmindre du begynder at tænke på ting som “Hvilken skal jeg bruge” eller “hvor lille skal det eksplicitte tidsforøgelse være”, og sådan noget. Ingen bekymringer, jeg har dig dækket!

lad os dykke ind!

dynamik på sit bedste – Implicit / eksplicit!

du vil bruge implicitte og eksplicitte løsere til at løse dynamiske problemer. Det betyder, at du ikke behøver at kende disse ting, hvis du laver statisk analyse., Hvis du er usikker på forskellen mellem statisk og dynamisk analyse, læs venligst dette indlæg først – det vil gøre tingene lettere at forstå!

Dynamisk analyse i en nøddeskal:

Dynamisk analyse løser problemer med inerti effekter. De vises, når tingene ændrer sig hurtigt i din model (hurtigt anvendte belastninger, påvirkninger osv.). Ingeniører henviser normalt til dette som”ikke-lineær dynamik”.

det skal bemærkes, at ingeniører ofte også kalder anden analyse “dynamisk”., Ting som Modal analyse eller tvungen respons analyse, der beskæftiger sig med vibrationer. Nogle gange kaldes de “lineær dynamik”, men det er normalt en god ide at sikre sig, hvad nogen betyder, når de bruger en sådan sætning. Mens” lineære dynamiske ” problemer er virkelig interessante, vil jeg ikke diskutere dem her. Du kan lære mere om dem, der læser dette indlæg!

det første, jeg virkelig føler, at jeg er nødt til at understrege, er, at implicitte og eksplicitte løsere løser de samme problemer!, Tænk på det ikke som “forskellige løsere”, men snarere som to forskellige måder at løse det samme problem på.

i mange tilfælde kan du bruge både implicit og eksplicit solver, og de vil give det samme resultat. Og jeg tror, det er her, vi skal starte!

hvordan dynamisk analyse virker?

begge analyser løser et problem, hvor tingenes hastighed er vigtig. Dette betyder for det meste, at belastningen påføres meget hurtigt. I sådanne tilfælde vil du altid “gentage” din belastning i tide., Dybest set vil du bruge tiden til at fortælle Løseren “Hvad sker der” og hvordan belastningen ændrer sig.for det første skal du definere, hvordan belastningen ændrer sig i tide. Du gør normalt dette ved hjælp af diagrammer, som den nedenfor:

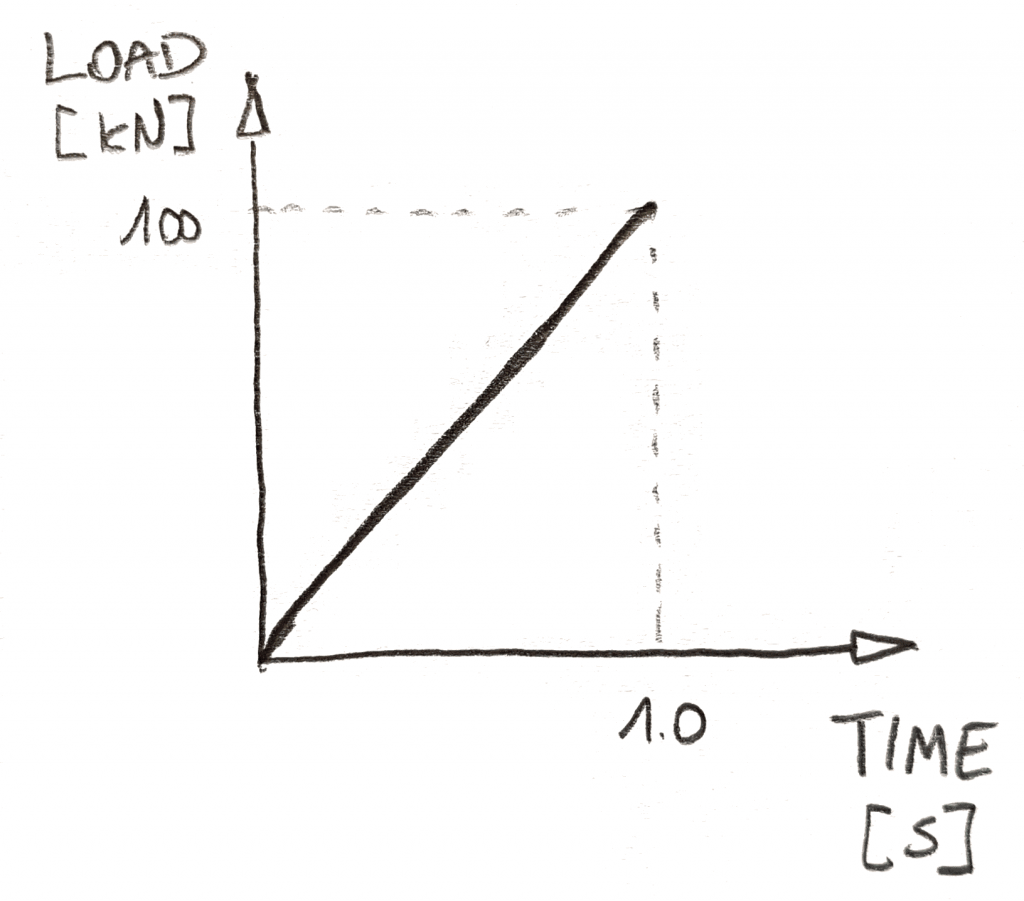
I ikke-lineær dynamisk analyse har tiden 2 roller. For det første giver det dig mulighed for at fortælle Løseren, hvornår hvor meget belastning der skal påføres. Du skal blot implementere hver belastning med et tidsafhængigt diagram. For det andet… tid er tid! Det fortæller solver, hvor hurtigt det går!,

Forestil dig, at du ønsker at have sådan en belastning sekvens:

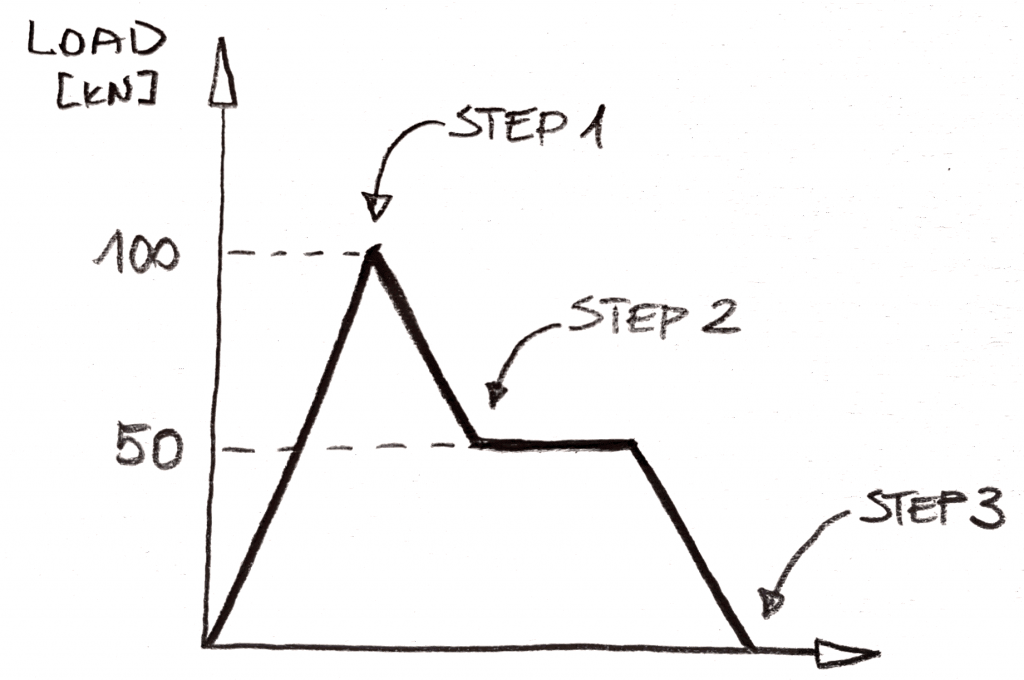
statisk, ville dette være en 3 “trin” analyse (disse kaldes subcases i NX Nastran, men jeg tror, at Abaqus faktisk brugt “trin” som et navn, kan ikke huske det dog sikkert!). Ideen ville være enkel, du skal anvende 100KN af belastningen i trin 1, fjern derefter 50kN af belastningen i trin 2, og fjern 50kN i trin 3. Der er ingen måde at medtage “plateau” af belastning efter trin 2 i analysen, og det vil blive udeladt., Logik er enkel: ingen ændringer i belastning = intet ændringer i statisk!

belastningstilstande i statisk

Hvis problemet ville være meget ikke-lineært, ville belastningen blive “forøget”. Det er sjældent at kunne anvende “fuld belastning” i ikke-lineær analyse på “one go”! Normalt ville solver anvende dvs. 1kN hver “tilvækst”. Dette betyder, at efter 100 trin, en fuld belastning af trin 1 ville blive anvendt. Dette gør det lettere for solver at konvergere et korrekt svar.,

som bruger får du defineret, hvor store trin solver skal bruge. Der er også nogle algorythms til at ændre belastningsforøgelse under analysen. Forskellige løsere vil have dig til at indstille dette på forskellige måder. Normalt bruger FEA-pakker belastningsmultiplikatorer til dette. Det betyder, at du kan sige noget i retning af:”i hvert trin gælder yderligere 0,01 af al belastning”.

fantastisk… men lad os komme til dynamik, skal vi?, I dynamisk analyse kan du få belastningsfordelingen som ovenfor med en sådan belastningsdefinition:

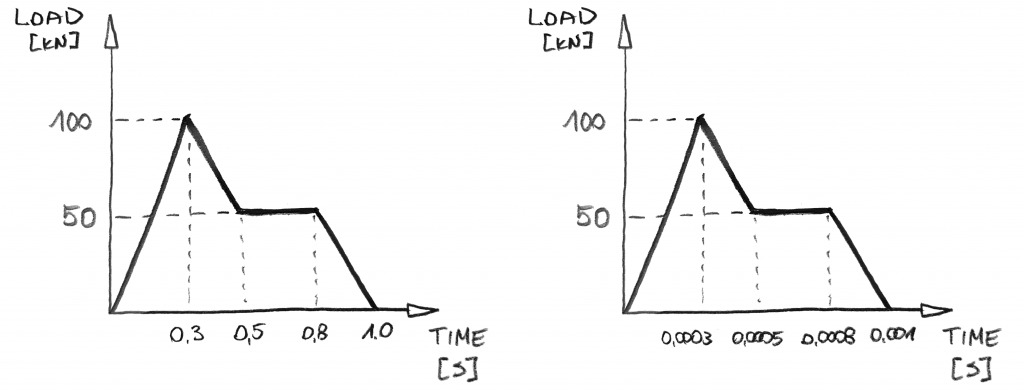
øjeblikkeligt er der et par ting, du kan bemærke:

• der er ingen trin! Dette skyldes, at du i dynamisk analyse ikke øger belastningen. Du vil øge tiden! Og da tiden går ” konstant “fra nul til den foreskrevne værdi, kan du øge den i”et trin”.

• tiden er af afgørende betydning! Når det kommer til værdierne af belastningen, er ovenstående diagrammer de samme., Men dette er ikke den samme dynamiske sag! Diagrammet til højre anvender belastningen 1000 quicker hurtigere! Dette er ikke noget, du bare kan ignorere i dynamisk analyse!

generelt, når du vil løse et dynamisk problem, beder du din solver om at gøre en ting. Du beder den om at beregne serien af tidsforøgelser for at se, hvad der foregår i modellen. I hvert af disse trin øges tiden lidt. Dette ændrer selvfølgelig også belastningen i modellen. Det er derfor, du har brug for at have en tidsafhængig diagram for belastning., Så solver “ved”, hvilken belastning der skal anvendes på hvilket tidspunkt stigning. For så vidt fungerer det på samme måde som belastningsforøgelse i statisk analyse. Bonussen er, at da du er stigende tid, inerti effekter kan tages i betragtning, når tingene sker hurtigt nok.

i dette omfang gør både implicit og eksplicit analyse mere eller mindre det samme. De deler “analysetiden” i små trin, og analyserer derefter, hvad der foregår i din model, en stigning af tid efter den anden. Men her er hvor lighederne slutter!, Du ser, der er forskellige tilgange til tidsforøgelse, du måtte have!

Implicit vs eksplicit-når tiden virkelig betyder noget!

, Du lige har lært, at for at beregne den ikke-lineære dynamiske problem, du bliver nødt til at gradvist øge “analyse”. Som jeg allerede nævnte, kan dette gøres på to måder.

Jeg vil starte med den implicitte tilgang. Jeg synes, det er lettere at forstå, da det fungerer mere eller mindre det samme som belastningsforøgelse i ikke-lineær statisk analyse!,

Sådan fungerer Implicit analyse:

først og fremmest synes implicit at være en mere “grundlæggende” løsning. I det væsentlige virker det lige som du ville synes det skal!

• for det første etableres den “globale ligevægt” i modellen i hver tidsforøgelse. Dette betyder, at hver stigning skal konvergere (dette sker i iterationer).

• når den globale ligevægt er ok, beregner solver alle de lokale endelige elementvariabler (stress osv.) for denne stigning.,

• fordele: da den globale ligevægt verificeres ved hver gang trin, kan disse trin være store!
• ulemper: hver gang stigning beregnes langsomt, da iterationer er nødvendige for at komme til den globale ligevægt.

Hvis du er bekendt med den ikke-lineære statiske analyse, vil du føle dig “hjemme” med den implicitte solver. Som bruger får du normalt at sige, hvor store de tidsintervaller du vil have. Dette er en enorm fordel … der er let at gå glip af., Fordi eksplicit solver ikke tilbyder en sådan mulighed!

lad os tage et kig på eksplicit incrementation næste!

Sådan fungerer eksplicit analyse:

denne er funky. Det virker på en måde, at du ikke behøver at konvergere hvert trin! Der er ingen konvergenskriterier at kontrollere og … ingen iterationer! I stedet for at verificere den “globale ligevægt” antager solver, at ligevægten “simpelthen eksisterer”. Det betyder, at solver går lige ind i beregningen af lokale finite element variabler!, Som sådan procedure har kun Stept trin:

• Beregn alle de lokale finite element variabler for given tilvækst, og flytte til den næste!

• fordele: hver stigning beregner ekstremt hurtigt!
• ulemper: for at dette skal fungere, skal tidstrinnet være ekstremt lille. Ellers er det umuligt at opretholde denne ligevægt, der antages at “simpelthen eksistere”. For at opnå dette, behøver brugeren ikke har direkte kontrol over, hvordan big-time intervaller eksplicit solver vil tage., Solver selv beregner, hvor små tidstrin er stadig ok. Og disse acceptable tidstrin er SUPER små! Dette er grunden til eksplicitte problemer bør sidste brøkdele af den anden! Hvis de ville vare sekunder … du ville have brug for millioner af trin!

for hurtigt at opsummere det: både implicitte og eksplicitte løsere løser de samme ting. Den eneste forskel er, hvordan disse metoder tilvækst tid.

teknisk set bør begge give det samme resultat for alle tilfælde., Når alt kommer til alt kan du analysere det samme problem med begge tilgange. Svaret kan naturligvis ikke afhænge af den metode, der bruges til at løse problemet! Men selvfølgelig vil du kun vælge en af tilgange til dit næste problem,så hvilken? Lad os finde ud af det!

Hvad er bedre for dig: Implicit eller eksplicit?

vi har allerede aftalt, at du kan bruge både implicitte og eksplicitte løsere til at løse den samme type problemer. Den eneste forskel er i tilgang til tidsforøgelse. Men det er ikke en triviel ting!, Hvis forskellen ville være lille, ville ingen passe på at implementere begge dele! Så lad os tage et kig på, hvordan denne gang incrementation påvirke tingene!

både implicitte og eksplicitte løsere har nogle områder, hvor de skinner. Og der er en overlapning i deres brug:

• den implicitte analyse giver dig mulighed for at vælge, hvor stor tidsforøgelsen skal være! Dette tilvækst vil tage nogen tid at beregne, da det skal gentage for global ligevægt først. Men du kan gøre det “rimeligt stort” til din analyse.,

• eksplicitte tidsintervaller Beregn virkelig hurtigt! Simpelthen fordi de ikke gentager sig for global ligevægt… men tidsforøgelsen der er ikke dit valg! Solver antager simpelthen, at den” acceptable “tidsforøgelse er” and ” og går med det. Bemærk, at denne” “” nemt kan være noget som 5e-7s… dette er super lille! For at løse et problem, der sker over 1s, skal du bruge 2 000 000 trin!

• og det er det! Hastigheden af computing er præcis forskellen mellem implicit og eksplicit., Selvfølgelig, størrelsen af eksplicit trin afhænger af din model og computing gange afhænger af din hard .are. Der er dog simple observationer, som vi kan nemt gøre:

Brug implicitte for “langsom analyse”!

hvis det, du beregner, sker over flere sekunder… er der ingen mening i at bruge eksplicit solver. Det vil tage for evigt at grave gennem de millioner af tidstrin, der er nødvendige for at dette kan beregne!, I stedet skal du indstille et “rimeligt” tidstrin for implicit analyse (lad os sige 100 lige tidsintervaller til din analyse). Jo da, hver af disse implicitte tid intervaller vil beregne meget længere end en enkelt eksplicit tilvækst. Men ikke længere end hundredtusinder af dem!

Brug eksplicit til “hurtig analyse”!

Dette er indlysende, ikke? Hvis det, du beregner, sker i den lille brøkdel af et sekund eksplicit, er din ven., I en implicit analyse ville din tidsforøgelse være super lille … måske endda så lille som stigningen i eksplicit analyse. I et sådant tilfælde eksplicit analyse vil køre meget hurtigere, da det ikke kræver “global ligevægt” iterationer. Den implicitte analyse kræver disse iterationer (uanset tidstrin!).

Inbetween ting!

selvfølgelig er der problemer, der sker i midten (som en påvirkning med 5m / s hastighed)., Normalt kan du løse et sådant problem med begge løsere, men det kan være irriterende.

jeg håber, at dette hjælper dig med at vælge en korrekt tilgang til dine dynamiske problemer. Selvfølgelig, i sidste ende, oplevelsen er den bedste guide! Hvis du er i tvivl, køre et par af dine typiske problemer i både implicit og eksplicit. På denne måde vil du være i stand til at sammenligne resultater (de skal være de samme). Men hvad er mere vigtigt, vil du være i stand til at sammenligne computing gange! Dette vil give dig en mulighed for at kontrollere, hvad er en bedre tilgang for dig!,

hvor eksplicit gætter tid trin størrelse?

nå, det er alt godt og dandy indtil videre, men jeg synes, det ville være rart at løse et stort problem. Og det er… hvis du ikke vælger tidstrinnet i din eksplicitte analyse … hvem gør så?

den matematiske forklaring ville kræve en diskussion om den maksimale naturlige frekvens. Dette skyldes, at maksimal “stadig acceptabel” tidsforøgelse er omvendt proportional med den maksimale naturlige frekvens. Sådanne beregninger kan selvfølgelig gøres., Resultaterne afhænger af modelens maske (hvor mange elementer er der osv.). Men vi går ikke der, og der er 2 grunde til: for det første kan jeg ikke lide matematik (!). For det andet er det ikke sådan, hvordan løsere gør det til sidst, selvom dette er den “rigtige måde”.

solveren kan selvfølgelig beregne den maksimale naturlige frekvens, men det tager lang tid. Og da det skulle gøres i hvert eksplicit tidsforøgelse (der kan være masser af dem!) … yikes!, Heldigvis er der en måde at pænt estimere denne værdi ved at analysere hvert endeligt element i systemet separat! Den fysiske fortolkning af dette skøn (almindeligvis anvendes i solvers) er:

Maksimal tid tilvækst i eksplicit analyse:

Tid tilvækst i eksplicit analyse, er meget kort. Det er den tid, hvor en elastisk bølge (dvs.slagbølge) kan rejse gennem et enkelt endeligt element i din model. Selvfølgelig er dette verificeret for alle endelige elementer i din model, og den mindste tid er valgt.,

Som du kan se, der er 2 komponenter til de eksplicitte tid komponent:

• Elastisk bølge hastighed (aka hastigheden af lyd i dit materiale)! Dette afhænger kun af det materiale, du har i din model (og det er anderledes for forskellige materialer selvfølgelig!). Du skal bruge den unge modul E, materiale tæthed og Poisson Ration (i 2D og 3D problemer). Det er nemt at finde tabeller, der viser elastiske bølgehastigheder i forskellige materialer. Bare for reference i stål er dette omkring 5200m/s (mange metaller er omkring 4500-5500m / s).,

• Elementstørrelse (og kvalitet)! Du har bølgehastigheden, men det er ikke nok! For at kende den tid, det har brug for at rejse gennem elementet, skal du kende elementet “længde”. Selvom dette er super simpelt i 1D-elementer (de har simpelthen længde), bliver det vanskeligt i 2D og 3D. denne længde er ikke “simpelthen” den korteste af elementkanterne, da elementer kan have temmelig dårlig geometri. Der er ting solver gør for at beregne dette. I 2D kan det være et elementområde divideret med den maksimale kantlængde., I 3D kan betyde, at elementets volumen er divideret med det maksimale sideområde. Derfor er ikke kun Elementstørrelse, men også elementkvalitet så vigtig i eksplicit analyse! Når alt kommer til alt … alt hvad du behøver er et dårligt element for virkelig at skade din computertid!

jeg har læst et sted, at mens ovenstående er den “præcise” løsning, bruger solvere ofte “sikkerhedsfaktorer” på dette. Hvis du får en højere tidsforøgelse end den elastiske bølge “hastighedsgrænse” forekommer matematiske fejl. Da estimater anvendes, reducerer løsere ofte tidstrinnet”bare i tilfælde”., Normalt er reduktionsfaktoren omkring 0,9, men det kan naturligvis variere fra solver til solver.

masse skalering!

i sidste ende vil jeg nævne noget hurtigt.

du har sandsynligvis bemærket, at tidstrinnet i eksplicit kun afhænger af nettet, ung modul og densitet. Reduktion af ung modul er måske ikke ideel selvfølgelig, og du har ofte brug for et lille maske til at analysere detaljer. Men i” lav dynamiske ” problemer kan du forsøge at øge det eksplicitte tidstrin ved at øge materialetætheden.,

dette kaldes “masseskalering”. FEA-pakker tilbyder endda løsninger, hvor tætheden kun øges i de elementer, der “beslutter” om tidsforøgelse. Det betyder, at nogle gange kun små portioner af din model bliver tungere! I nogle analyser kan du “komme væk” med at øge massen af din model. Hvis det er tilfældet, kan dette være en løsning for dig. Bare vær opmærksom på, at dette ændrer, hvordan din model opfører sig! Når der er tale om høje accelerationer, er det bedst at være forsigtig!

Oversigt

Nice!, Du fik her, tak for læsning! Lad os pakke det op, så det er lettere at huske!

• dynamisk analyse involverer tid! Når du anvender belastninger, skal de defineres i en tidsfunktion. Ofte er dette en lineær relation. Men det ændrer sig ikke, at den tid, hvor belastningen påføres, spiller en væsentlig rolle (især hvis denne tid er kort!).

• 2 varianter af dynamisk analyse! Du kan løse de “rigtige” dynamiske problemer med implicitte og eksplicitte algoritmer. Begge er fine, og ikke en eneste af dem er “bedre”., Men jeg skal sige, at den eksplicitte solver er en del af færre FEA-pakker. Da ikke alle FEA-pakker endda har en, ses den eksplicitte solver som en “mere avanceret” ting.

• den implicitte solver er virkelig god, hvis ting i din analyse sker relativt langsomt. Lad os sige analyse er længere end 1s uden nogen pludselige ting sker i løbet af denne tid. Fordelen er, at du kan vælge, hvor stor tidsforøgelsen du ønsker. Selv hvis den enkelte tilvækst tager længere tid at beregne, der er langt færre af dem!,

• den eksplicitte solver er fantastisk til hurtige ting (lad os sige hurtigere end 0.1 s). Du får ikke mulighed for at vælge tidsforøgelsen her – solver indstiller den automatisk. Mens de normalt er super små, beregner de i det mindste meget hurtigere end de “implicitte”. Eksplicit solver beregner, hvor stor tidsforøgelsen skal være. Dette afhænger af lydhastigheden i dit materiale, minimal endelig Elementstørrelse (og elementkvalitet!). I nogle tilfælde kan du ændre tæthed (selv automatisk kun i “afgørende elementer”!) for at justere denne tidsforøgelse., Dette fungerer, fordi lydens hastighed i dit materiale afhænger af dens densitet! Dette kaldes “masseskalering”.