Good Mood

beeld je dit in: je maakt een presentatie van je Ph.D. thesis over stabiliteit tijdens een van de seminars. Alles verloopt soepel en tot slot is het vragenuur. En iemand uit het niets vraagt: “Wat is het verschil tussen impliciete en expliciete benadering?”! En aangezien je statische stabiliteit doet … heb je die termen nog nooit gehoord! Ja … dat heb ik al eens gedaan!, Nu, ik ben een beetje wijzer, dus laten we eens een kijkje nemen op de verschillen tussen impliciete en expliciete analyse

impliciete en expliciete analyse verschillen in de benadering van tijd incrementatie. In impliciete analyse moet elke keer increment convergeren, maar je kunt vrij lange tijd increments instellen. Expliciet aan de andere kant hoeft niet te convergeren elke increment, maar voor de oplossing om nauwkeurige tijd stappen moeten super klein zijn.

Dit klinkt vrij eenvoudig, toch?, Tenzij je begint na te denken over dingen als “welke moet ik gebruiken” of “hoe klein moet de expliciete tijd toename zijn”, en dat soort dingen. Geen zorgen, Ik heb je gedekt!

laten we erin duiken!

dynamiek op zijn best-impliciet / expliciet!

U zult impliciete en expliciete oplossers gebruiken om dynamische problemen op te lossen. Dit betekent dat u dit materiaal niet hoeft te weten als u statische analyse doet., Als u niet zeker bent over het verschil tussen statische en dynamische analyse, lees dan dit bericht eerst – het zal dingen gemakkelijker te begrijpen!

dynamische analyse in een notendop:

dynamische analyse lost problemen met inertie-effecten op. Die verschijnen, wanneer dingen snel veranderen in uw model (snel toegepaste belastingen, impacts, enz.). Ingenieurs meestal reffer naar dit als “niet-lineaire dynamic”.

Opgemerkt dient te worden dat ingenieurs ook andere analyses” dynamisch ” noemen., Dingen zoals modale analyse of geforceerde respons analyse die omgaan met trillingen. Soms worden die “Lineaire dynamiek” genoemd, maar het is meestal een goed idee om er zeker van te zijn wat iemand bedoelt als hij een dergelijke uitdrukking gebruikt. Hoewel “lineaire dynamische” problemen echt interessant zijn, zal ik die hier niet bespreken. U kunt meer over hen lezen van dit bericht leren!

het eerste wat ik echt moet benadrukken is dat impliciete en expliciete oplossers dezelfde problemen oplossen!, Zie het niet als “verschillende oplossers” maar eerder als twee verschillende manieren om hetzelfde probleem op te lossen.

in veel gevallen kunt u zowel impliciete als expliciete oplosser gebruiken, en ze zullen hetzelfde resultaat produceren. En ik denk dat we hier moeten beginnen!

Hoe werkt dynamische analyse?

beide analyses lossen een probleem op waarbij de snelheid van dingen belangrijk is. Dit betekent meestal dat de belasting zeer snel wordt toegepast. In dergelijke gevallen zult u uw lading altijd op tijd “herhalen”., In principe zul je de tijd gebruiken om de oplosser te vertellen “wat er gebeurt” en hoe de belasting verandert.

ten eerste moet u definiëren hoe de belasting in de tijd verandert. U doet dit meestal met behulp van grafieken, zoals hieronder:

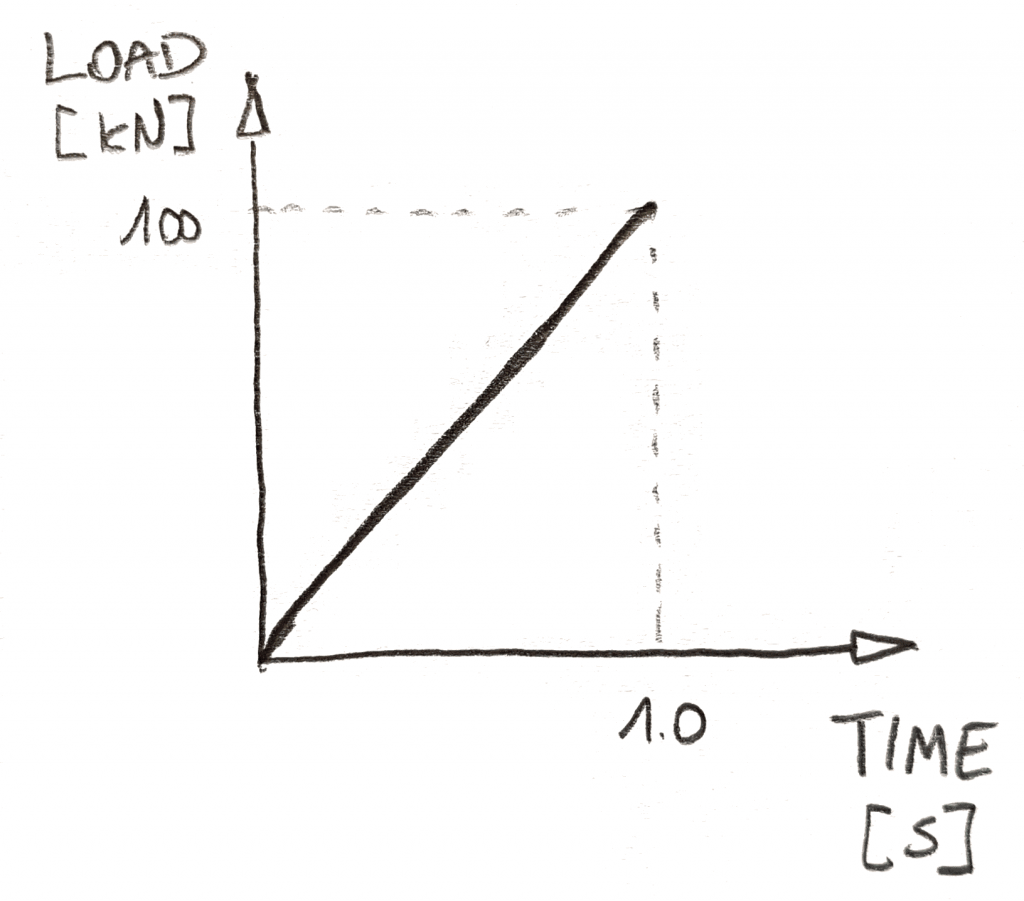
In niet-lineaire dynamische analyse heeft de tijd 2 rollen. Ten eerste kunt u de oplosser vertellen wanneer hoeveel belasting moet worden toegepast. Je hoeft alleen maar om elke belasting te implementeren met een tijd-afhankelijke grafiek. Ten tweede … tijd is tijd! Het vertelt de oplosser hoe snel dingen gaan!,

stel je voor dat je zo ‘ N load sequence wilt hebben:

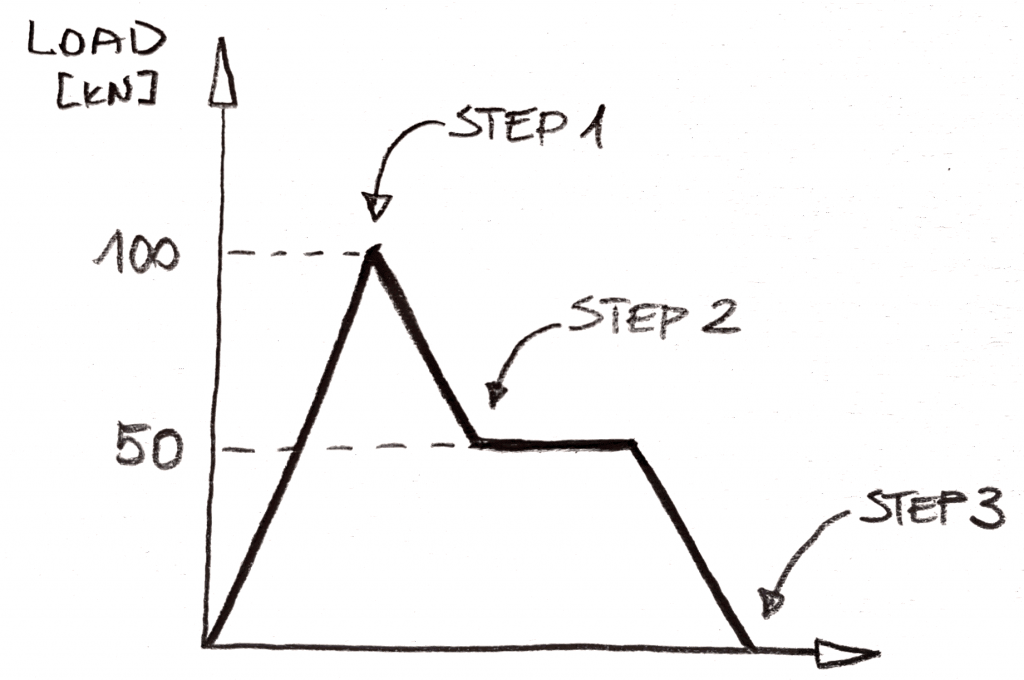
in static zou dit een 3 “steps” analyse zijn (deze worden subcases genoemd in NX Nastran, maar ik denk dat Abaqus eigenlijk “step” als naam gebruikt heeft, kan dit echter niet met zekerheid herinneren!). Het idee zou eenvoudig zijn, je moet de 100kn van de belasting in Stap 1 toe te passen, verwijder dan 50kN van de belasting in Stap 2, en verwijder 50kN in Stap 3. Er is geen manier om het “plateau” van belasting na stap 2 in de analyse op te nemen, en het zal worden weggelaten., Logica is eenvoudig: geen veranderingen in belasting = niets verandert in statisch!

belastingverhogingen in statisch

als het probleem zeer niet-lineair zou zijn, zou de belasting worden”verhoogd”. Het is zeldzaam om “full load” toe te passen in niet-lineaire analyse op “one go”! Meestal, oplosser zou toepassen dwz 1kN elke “increment”. Dit betekent dat na 100 stappen, een volledige belasting van stap 1 zou worden toegepast. Dit maakt het makkelijker voor de oplosser om een juist antwoord te convergeren.,

als gebruiker kunt u bepalen hoe grote stappen oplosser moet gebruiken. Er zijn ook enkele algorythmen om de belastingverhoging tijdens de analyse te wijzigen. Verschillende oplossers willen dat je dit op verschillende manieren instelt. Gewoonlijk gebruiken FEA-pakketten hiervoor load multipliers. Dit betekent, dat je iets kunt zeggen als:”in elke verhoging toe te passen extra 0,01 van alle belasting”.

Awesome … maar laten we naar dynamics gaan, zullen we?, In dynamische analyse kunt u de verdeling van de belasting zoals hierboven met een dergelijke load definitie krijgen:

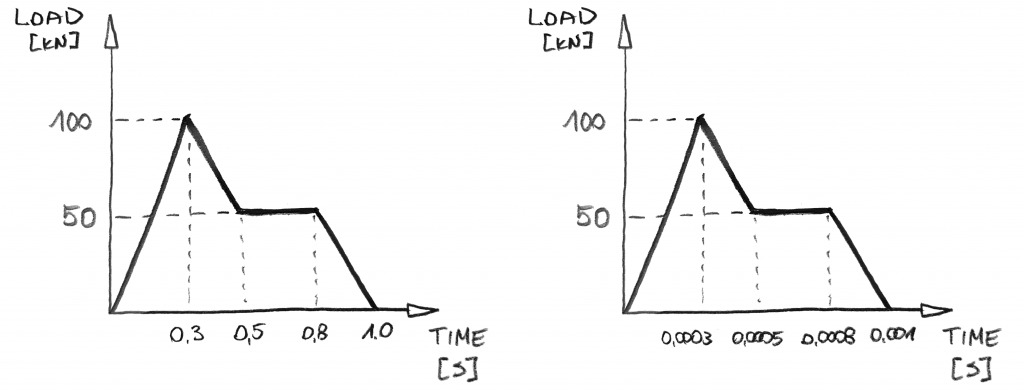
direct, er zijn een paar dingen die u kunt opmerken:

• er zijn geen stappen! Dit komt omdat u in dynamische analyse niet de belasting verhoogt. Je zal de tijd verhogen! En omdat de tijd “constant” gaat van nul naar de voorgeschreven waarde, kunt u deze in “één stap”verhogen.

• tijd is essentieel! Als het gaat om de waarden van de belasting, de bovenstaande grafieken zijn hetzelfde., Maar dit is niet hetzelfde dynamische geval! De grafiek aan de rechterkant past de belasting 1000x sneller toe! Dit is niet iets wat je gewoon kunt negeren in dynamische analyse!

in het algemeen, wanneer u een dynamisch probleem wilt oplossen, vraagt u uw oplosser om één ding te doen. Je vraagt het om de reeks tijdsverhogingen te berekenen, om te zien wat er in het model gebeurt. In elk van deze stappen neemt de tijd licht toe. Dit verandert natuurlijk ook de belasting in het model. Dit is de reden waarom je nodig hebt om een tijd-afhankelijke grafiek voor de belasting., Dus de oplosser “weet” welke belasting moet worden toegepast op welk moment increment. In deze mate werkt het hetzelfde als belastingverhoging in statische analyse. De bonus is, dat omdat je het verhogen van de tijd, inertie-effecten kan worden rekening gehouden wanneer dingen snel genoeg gebeuren.

in deze mate doet zowel impliciete als expliciete analyse min of meer hetzelfde. Ze verdelen de” analysetijd ” in kleine stappen en analyseren vervolgens wat er in uw model gebeurt, de ene stap na de andere. Maar hier is waar de overeenkomsten eindigen!, Zie je, er zijn verschillende benaderingen van tijd incrementatie die je kan hebben!

impliciet vs expliciet-Wanneer tijd er echt toe doet!

U hebt zojuist geleerd dat u, om het niet-lineaire dynamische probleem te berekenen, de”analysetijd” stapsgewijs moet verhogen. Zoals ik al zei, kan dit op twee manieren gebeuren.

Ik zal beginnen met de impliciete benadering. Ik denk dat het gemakkelijker te begrijpen, omdat het werkt min of meer hetzelfde als belasting incrementatie in niet-lineaire statische analyse!,

Hoe werkt impliciete analyse:

allereerst lijkt impliciet een meer” basis ” oplossing te zijn. In essentie werkt het precies zoals je zou denken dat het zou moeten!

• Ten eerste wordt in elke stap het” globaal evenwicht ” in het model vastgesteld. Dit betekent dat elke increment moet convergeren (dit gebeurt in iteraties).

• nadat het globale evenwicht ok is, berekent solver alle lokale eindige-elementenvariabelen (spanningen enz.) voor deze verhoging.,

• voordelen: aangezien het globale evenwicht telkens wordt gecontroleerd, kunnen deze verhogingen groot zijn!
• nadelen: elke keer wordt de toename langzaam berekend, omdat iteraties nodig zijn om tot het globale evenwicht te komen.

Als u bekend bent met de niet-lineaire statische analyse, zult u zich” thuis ” voelen met de impliciete oplosser. Als gebruiker, krijg je meestal om te zeggen hoe groot de tijd stappen die u wilt hebben. Dit is een enorm voordeel… dat makkelijk te missen is., Want Explicit solver biedt zo ‘ n mogelijkheid niet!

laten we een kijkje nemen op expliciete incrementatie volgende!

Hoe werkt expliciete analyse:

deze is funky. Het werkt op een manier, dat je niet hoeft te convergeren elke stap! Er zijn geen convergentiecriteria om te controleren en … geen herhalingen! In plaats van de “globaal evenwicht” te verifiëren, gaat de oplosser ervan uit dat het evenwicht “eenvoudig bestaat”. Dit betekent dat de oplosser rechtstreeks in de berekening van lokale eindige elementen variabelen gaat!, Als zodanig heeft de procedure maar één stap:

• bereken alle lokale eindige elementenvariabelen voor een gegeven toename, en ga naar de volgende!

• voordelen: elke verhoging berekent extreem snel!
• nadelen: om dit te laten werken, moet de tijdsstap extreem klein zijn. Anders is het onmogelijk om dit evenwicht te handhaven dat verondersteld wordt “gewoon te bestaan”. Om dit te bereiken, heeft de gebruiker geen directe controle over hoe big-time increments explicit solver zal nemen., Solver zelf berekent hoe kleine timesteps zijn nog steeds ok. En die aanvaardbare tijdstappen zijn SUPER klein! Dit is de reden waarom expliciete problemen fracties van de tweede moeten duren! Als ze seconden zouden duren … zou je miljoenen stappen nodig hebben!

om het snel samen te vatten: zowel impliciete als expliciete oplossers lossen hetzelfde op. Het enige verschil is, hoe deze methoden verhogen tijd.

technisch gezien moeten beide voor alle gevallen hetzelfde resultaat opleveren., Immers, u kunt hetzelfde probleem met beide benaderingen te analyseren. Uiteraard kan het antwoord niet afhangen van de methode die wordt gebruikt om het probleem op te lossen! Maar natuurlijk kies je maar één van de benaderingen voor je volgende probleem, dus welke? Laten we dat uitzoeken!

Wat is beter voor u: impliciet Of expliciet?

we zijn al overeengekomen dat u zowel impliciete als expliciete oplossers kunt gebruiken om hetzelfde type problemen op te lossen. Het enige verschil is in benadering van tijd incrementatie. Maar het is geen triviale zaak!, Als het verschil klein zou zijn, zou niemand de zorg om beide te implementeren! Dus laten we eens kijken naar hoe deze tijd incrementatie van invloed dingen!

zowel impliciete als expliciete solvers hebben een aantal gebieden waar ze schitteren. En er is een overlap in hun gebruik:

• met de impliciete analyse kunt u kiezen hoe groot de tijdverhoging moet zijn! Deze verhoging zal enige tijd vergen om te berekenen aangezien het eerst voor globaal evenwicht moet herhalen. Maar je kunt het “redelijk groot” maken voor je analyse.,

• expliciete tijdstappen bereken heel snel! Gewoon omdat ze niet herhalen voor globaal evenwicht … maar de tijd toename daar is niet jouw keuze! Solver gaat er gewoon vanuit, dat de “aanvaardbare” tijd increment is “X” en gaat met het. Merk op, dat deze “X” kan gemakkelijk iets als 5e-7s … dit is super klein! Om een probleem op te lossen dat meer dan 1s gebeurt, zou je 2 000 000 stappen nodig hebben!

• en dat is het! De snelheid van het berekenen is precies het verschil tussen impliciet en expliciet., Natuurlijk, de grootte van expliciete stap is afhankelijk van uw model en computertijden is afhankelijk van uw hardware. Er zijn echter eenvoudige observaties die we gemakkelijk kunnen maken:

gebruik impliciet voor”slow analysis”!

als het ding dat je berekent over enkele seconden gebeurt… heeft het geen zin om expliciete oplosser te gebruiken. Het zal eeuwig duren om te graven door de miljoenen tijd increments die nodig zijn om dit te berekenen!, In plaats daarvan, stel een “redelijke” tijd stap voor impliciete analyse (laten we zeggen 100 gelijke tijd stappen voor uw analyse). Zeker, elk van deze impliciete tijd incrementen zal veel langer dan een enkele expliciete increment berekenen. Maar niet langer dan honderdduizenden!

Use explicit for”fast analysis”!

Dit is duidelijk, toch? Als wat je berekent gebeurt in de kleine fractie van een tweede expliciete is je vriend., In een impliciete analyse, zou je tijd increment super klein zijn … misschien zelfs zo klein als de increment in expliciete analyse. In zo ‘ n geval zal de expliciete analyse veel sneller verlopen omdat er geen “globaal evenwicht” iteraties nodig zijn. De impliciete analyse vereist deze herhalingen (ongeacht de tijdsstap!).

tussen spullen!

natuurlijk zijn er problemen in het midden (zoals een impact met 5m/s snelheid)., Meestal kunt u een dergelijk probleem met beide oplossers oplossen, maar het kan vervelend zijn.

ik hoop dat dit U helpt om een juiste aanpak van uw dynamische problemen te selecteren. Natuurlijk, op het einde, de ervaring is de beste gids! Als u in twijfel, run een paar van uw typische problemen in zowel impliciet Als expliciet. Op deze manier, zult u in staat zijn om resultaten te vergelijken (ze moeten hetzelfde zijn). Maar wat belangrijker is, je zult in staat zijn om computertijden te vergelijken! Dit geeft u een kans om te controleren, wat is een betere aanpak voor u!,

hoe expliciet gist de grootte van de tijdstap?

nou, het is allemaal leuk en dandy tot nu toe, maar ik denk dat het leuk zou zijn om een groot probleem aan te pakken. En dat is … als je niet de tijdstap selecteert in je expliciete analyse… wie dan wel?

de wiskundige uitleg vereist een discussie over de maximale natuurlijke frequentie. Dit komt omdat de maximale” nog steeds aanvaardbare ” tijdverhoging omgekeerd evenredig is met de maximale natuurlijke frequentie. Dergelijke berekeningen kunnen worden gedaan, natuurlijk., De uitkomsten zijn afhankelijk van de mazen van het model (hoeveel elementen zijn er, enz.). Maar we gaan er niet heen, en er zijn 2 redenen waarom: ten eerste, Ik hou niet van wiskunde (!). Ten tweede is dit niet hoe solvers het uiteindelijk doen, ook al is dit de”juiste manier”.

de oplosser kan natuurlijk de maximale natuurlijke frequentie berekenen, maar dit kost nogal wat tijd. En aangezien het zou moeten worden gedaan in elke expliciete tijd increment (er kunnen tal van die!) … jakkes!, Gelukkig is er een manier om deze waarde mooi in te schatten, door elk eindig element in het systeem afzonderlijk te analyseren! De fysische interpretatie van deze schatting (vaak gebruikt in solvers) is:

maximale tijdverhoging in expliciete analyse:

Tijdverhoging in expliciete analyse is zeer kort. Het is de tijd waarin een elastische golf (dat wil zeggen impact golf) kan reizen door een enkel eindig element van uw model. Natuurlijk wordt dit geverifieerd voor alle eindige elementen in uw model, en de kleinste tijd wordt geselecteerd.,

zoals u kunt zien, zijn er 2 componenten aan de expliciete tijdcomponent:

• elastische golfsnelheid (aka geluidssnelheid in uw materiaal)! Dit hangt alleen af van het materiaal dat je in je model hebt (en het is natuurlijk anders voor verschillende materialen!). Je hebt de jonge Modulus E, materiaaldichtheid en Poisson rantsoen nodig (in 2D en 3D problemen). Het is gemakkelijk om tabellen te vinden met elastische golfsnelheden in verschillende materialen. Alleen voor referentie in staal, Dit is ongeveer 5200m/s (veel metalen zijn ongeveer 4500-5500m / s).,

• Elementgrootte (en kwaliteit)! Je hebt de golfsnelheid, maar het is niet genoeg! Om de tijd te kennen die het nodig heeft om door het element te reizen, moet u het element “lengte”kennen. Hoewel dit super eenvoudig is in 1D-elementen (ze hebben gewoon lengte) wordt het lastig in 2D en 3D. Deze lengte is niet “simpelweg” de kortste rand van het element, omdat elementen een vrij slechte geometrie kunnen hebben. Er zijn dingen die solver doet om dit te berekenen. In 2D kan het een element gebied gedeeld door de maximale randlengte., In 3D kan het betekenen dat het volume van het element wordt gedeeld door het maximale zijoppervlak. Daarom is niet alleen de grootte van de elementen, maar ook de kwaliteit van de elementen zo belangrijk in expliciete analyse! Immers … alles wat je nodig hebt is een arm element om echt pijn uw computer tijd!

ik heb ergens gelezen dat hoewel het bovenstaande De” precieze “oplossing is, solvers vaak” veiligheidsfactoren ” gebruiken. Als je een hogere tijd toename dan de elastische golf “snelheidslimiet” wiskundige fouten optreden. Aangezien schattingen worden gebruikt, solvers vaak verminderen de tijd stap”voor het geval”., Meestal ligt de reductiefactor rond 0,9, maar dit kan natuurlijk variëren van oplosser tot oplosser.

massaschaling!

op het einde wil ik iets snel vermelden.

U hebt waarschijnlijk gemerkt dat de tijdsstap in expliciete alleen afhangt van de mesh, jonge Modulus en dichtheid. Het verminderen van jonge Modulus kan natuurlijk niet ideaal zijn, en je hebt vaak een klein gaas nodig om details te analyseren. Maar in” low dynamic ” problemen kun je proberen om de expliciete tijd stap te verhogen door het verhogen van de materiële dichtheid.,

dit wordt”mass scaling” genoemd. FEA-pakketten bieden zelfs oplossingen waarbij de dichtheid alleen wordt verhoogd in de elementen die “beslissen” over tijdverhoging. Dit betekent dat soms slechts kleine porties van uw model zwaarder worden! In sommige analyses kunt u” wegkomen ” met het verhogen van de massa van uw model. Als dat het geval is kan dit een oplossing voor u zijn. Wees er gewoon van bewust, dat dit verandert hoe uw model zich gedraagt! Bij hoge versnellingen is het het beste om voorzichtig te zijn!

Summary

Nice!, Je bent er, bedankt voor het lezen! Laten we dit afronden, zodat het makkelijker is om te onthouden!

• dynamische analyse heeft tijd nodig! Wanneer u belastingen toepast, moeten deze worden gedefinieerd in een tijdfunctie. Vaak is dit een lineaire relatie. Maar dit verandert niet, dat de tijd waarin belasting wordt toegepast een belangrijke rol speelt (vooral als deze tijd kort is!).

• 2 Smaken van dynamische analyse! Je kunt de “echte” dynamische problemen oplossen met impliciete en expliciete algoritmen. Beide zijn prima, en geen enkele van hen is “beter”., Maar ik moet zeggen dat de expliciete oplosser deel uitmaakt van minder FEA-pakketten. Omdat niet elk FEA-pakket er één heeft, wordt de expliciete oplosser gezien als een” geavanceerder ” ding.

• de impliciete oplosser is echt goed als dingen in uw analyse relatief langzaam gebeuren. Laten we zeggen dat de analyse langer is dan 1s zonder abrupte dingen gebeuren gedurende die tijd. Het voordeel is dat u kunt kiezen hoe groot de tijd increment die u wilt. Zelfs als de enkele increment langer duurt om te berekenen, zijn er veel minder van hen!,

• de expliciete oplosser is geweldig voor snelle dingen (laten we zeggen sneller dan 0.1 s). U hoeft niet te kiezen voor de tijd increment hier-solver zal automatisch instellen. Hoewel ze meestal super klein zijn, berekenen ze in ieder geval veel sneller dan de “impliciete”. Explicit solver berekent hoe groot de tijd increment moet zijn. Dit hangt af van de geluidssnelheid in uw materiaal, minimale eindige elementgrootte (en elementkwaliteit!). In sommige gevallen kunt u de dichtheid wijzigen (zelfs automatisch alleen in “beslissende elementen”!) om deze tijdverhoging aan te passen., Dit werkt, want de snelheid van het geluid in uw materiaal hangt af van de dichtheid! Dit wordt “mass scaling”genoemd.