Pokaż komunikat mobilny Pokaż wszystkie notatki Ukryj wszystkie notatki
sekcja 4-6 : kształt wykresu, Część II
w poprzedniej sekcji widzieliśmy, jak możemy użyć pierwszej pochodnej funkcji, aby uzyskać informacje o wykresie funkcji. W tej sekcji przyjrzymy się informacji, że druga pochodna funkcji może dać nam o wykresie funkcji.
zanim to zrobimy, będziemy potrzebować kilku definicji. Główną koncepcją, którą omówimy w tej sekcji, jest wklęsłość. Wklęsłość najłatwiej zobaczyć na wykresie (za chwilę podamy definicję matematyczną).,
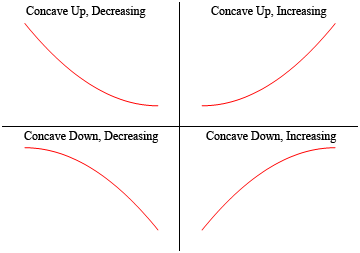
tak więc funkcja jest wklęsła w górę, jeśli „otwiera się” w górę, a funkcja jest wklęsła w dół, jeśli „otwiera się” w dół. Zauważ również, że wklęsłość nie ma nic wspólnego z rosnącym lub malejącym. Funkcja może być wklęsła i rosnąca lub malejąca. Podobnie, funkcja może być wklęsła w dół i rosnąca lub malejąca.
prawdopodobnie nie jest to najlepszy sposób na zdefiniowanie wklęsłości, mówiąc, w którą stronę się „otwiera”, ponieważ jest to nieco mglista definicja. Oto matematyczna definicja wklęsłości.,
definicja 1
aby pokazać, że powyższe wykresy faktycznie mają wklęsłość, o której mowa powyżej, tutaj znowu jest wykres (trochę rozwalony, aby wszystko było jaśniejsze).
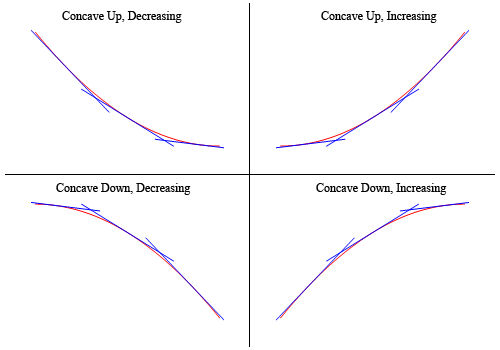
Tak więc, jak widać, na dwóch górnych wykresach wszystkie linie styczne naszkicowane są poniżej wykresu funkcji i są wklęsłe do góry. W dwóch dolnych wykresach wszystkie linie styczne znajdują się powyżej wykresu funkcji, a te są wklęsłe w dół.,
ponownie zauważ, że wklęsłość i rosnący/malejący aspekt funkcji są całkowicie oddzielne i nie mają ze sobą nic wspólnego. Jest to ważne, ponieważ uczniowie często mieszają te dwa i wykorzystują informacje o jednym, aby uzyskać informacje o drugim.
jest jeszcze jedna definicja, którą musimy usunąć.
definicja 2
punkt \(x = c\) nazywa się punktem przegięcia, jeśli funkcja jest ciągła w punkcie, a wklęsłość wykresu zmienia się w tym punkcie.,
teraz, gdy mamy wszystkie definicje konkwisty, musimy wprowadzić drugą pochodną do miksu. W końcu zaczęliśmy od tej sekcji mówiąc, że będziemy używać drugiej pochodnej, aby uzyskać informacje o wykresie. Następujący fakt odnosi się do drugiej pochodnej funkcji do jej wklęsłości. Dowód tego faktu znajduje się w sekcji dowody z zastosowań pochodnych w rozdziale Dodatki.
fakt
tak więc, co ten fakt mówi nam jest to, że punkty przegięcia będą wszystkie punkty były drugim znakiem zmiany pochodnej., Widzieliśmy w poprzednim rozdziale, że funkcja może zmieniać znaki, jeśli jest zerowa lub nie istnieje. Zauważ, że pracowaliśmy z pierwszą pochodną w poprzedniej sekcji, ale fakt, że funkcja ewentualnie zmieniająca znaki, gdzie jest zerowa lub nie istnieje, nie ma nic wspólnego z pierwszą pochodną. Jest to po prostu fakt, który odnosi się do wszystkich funkcji, niezależnie od tego, czy są pochodnymi, czy nie.,
to z kolei mówi nam, że lista możliwych punktów przegięcia będzie tymi punktami, w których druga pochodna jest równa zero lub nie istnieje, ponieważ są to jedyne punkty, w których druga pochodna może zmienić znak.
należy jednak uważać, aby nie zakładać, że tylko dlatego, że druga pochodna jest zerowa lub nie istnieje, że punkt będzie punktem przegięcia. Wiemy tylko, że jest to punkt przegięcia, gdy określimy wklęsłość po obu jego stronach. Będzie to tylko punkt przegięcia, jeśli wklęsłość jest inna po obu stronach punktu.,
teraz, gdy wiemy o wklęsłości, możemy użyć tych informacji, jak również informacji rosnących/malejących z poprzedniej sekcji, aby uzyskać całkiem dobre wyobrażenie o tym, jak powinien wyglądać Wykres. Spójrzmy na przykład.
możemy użyć poprzedniego przykładu, aby zilustrować inny sposób klasyfikacji niektórych punktów krytycznych funkcji jako względne maksimum lub względne minimum.
jak zobaczymy za chwilę będziemy musieli być bardzo ostrożni z \(x = 0\)., W tym przypadku druga pochodna wynosi zero, ale to nie oznacza, że \(x = 0\) nie jest względnym minimum lub maksimum. Za chwilę zobaczymy kilka przykładów, ale najpierw musimy zająć się innymi informacjami.
ważne jest również, aby zauważyć tutaj, że wszystkie punkty krytyczne w tym przykładzie były punktami krytycznymi, w których pierwsza pochodna wynosiła zero i jest to wymagane, aby to działało. Nie będziemy w stanie użyć tego testu w punktach krytycznych, w których pochodna nie istnieje.,
Oto test, który można wykorzystać do klasyfikacji niektórych punktów krytycznych funkcji. Dowód tego testu znajduje się w sekcji dowody zastosowań pochodnych w rozdziale Dodatki.
drugi test Pochodny
trzecia część drugiego testu pochodnego jest ważna do odnotowania. Jeśli druga pochodna jest równa zero, to punkt krytyczny może być dowolny. Poniżej znajdują się wykresy trzech funkcji, z których wszystkie mają punkt krytyczny w \(x = 0\), druga pochodna wszystkich funkcji wynosi zero W \(x = 0\), a jednak wszystkie trzy możliwości są pokazane.,
pierwszy to Wykres \(f \ left (x \right) = {x^4}\). Wykres ten ma względne minimum przy \(x = 0\).
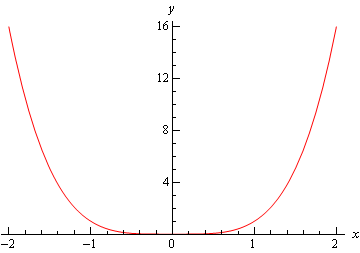
następny jest wykres \(f\left( x \right) = – {x^4}\), który ma względne maksimum w \(x = 0\).

wreszcie istnieje Wykres \(f\left( x \right) = {x^3}\) i ten wykres nie miał ani względnego minimum, ani względnego maksimum w \(x = 0\).
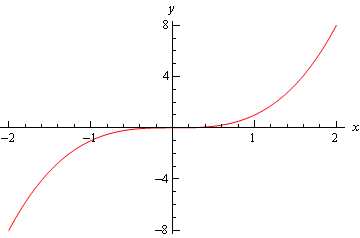
widzimy więc, że musimy być ostrożni, jeśli wpadniemy w trzeci przypadek., W tych czasach, kiedy wpadniemy w ten przypadek, będziemy musieli uciekać się do innych metod klasyfikacji punktu krytycznego. Zwykle odbywa się to za pomocą pierwszego testu pochodnego.
wróćmy i przyjrzyjmy się krytycznym punktom z pierwszego przykładu i wykorzystajmy drugi test Pochodny na nich, jeśli to możliwe.
popracujmy jeszcze nad jednym przykładem.















