Good Mood

obraz tego: robisz prezentację swojej pracy doktorskiej na temat stabilności na jednym z seminariów. Wszystko idzie gładko, a w końcu czas na pytania! I ktoś ni stąd ni zowąd pyta: „jaka jest różnica między podejściem niejawnym a jawnym?”! A skoro robisz statyczną stabilizację … nigdy nawet nie słyszałeś tych określeń! Tak … już to robiłem!, Teraz jestem nieco mądrzejszy, więc przyjrzyjmy się bliżej różnicom między analizą Implicit i Explicit

Analiza Implicit i Explicit różnią się podejściem do przyrostu czasu. W analizie Implicit za każdym razem przyrost musi się zbiegać, ale można ustawić dość długi przyrost czasu. Jawny z drugiej strony nie musi zbiegać każdy przyrost, ale dla rozwiązania, aby być dokładne przyrosty czasu muszą być bardzo małe.

To brzmi dość prosto, prawda?, Chyba, że zaczniesz myśleć o rzeczach takich jak „którego z nich powinienem użyć” lub „jak mały powinien być wyraźny przyrost czasu” i podobnych rzeczach. Nie martw się, zajmę się tobą!

zapraszam!

dynamika w najlepszym wydaniu-Implicit/Explicit!

do rozwiązywania problemów dynamicznych użyjesz ukrytych i jawnych rozwiązań. Oznacza to, że nie musisz tego wiedzieć, jeśli wykonujesz analizę statyczną., Jeśli nie masz pewności co do różnicy między analizą statyczną i dynamiczną, przeczytaj najpierw ten post – ułatwi to zrozumienie!

analiza dynamiczna w skrócie:

analiza dynamiczna rozwiązuje problemy związane z efektami bezwładności. Pojawiają się one, gdy rzeczy zmieniają się szybko w modelu (szybko stosowane obciążenia, uderzenia itp.). Inżynierowie zwykle określają to jako „nieliniową dynamikę”.

należy zauważyć, że często inżynierowie nazywają inne analizy również „dynamicznymi”., Takie rzeczy jak analiza modalna lub wymuszona analiza reakcji, które zajmują się wibracjami. Czasami są one nazywane „dynamiką liniową”, ale zwykle dobrym pomysłem jest upewnienie się, co ktoś ma na myśli, gdy używa takiego wyrażenia. Chociaż problemy „liniowej dynamiki” są naprawdę interesujące, Nie będę o nich tutaj dyskutował. Możesz dowiedzieć się więcej o nich czytając ten post!

pierwszą rzeczą, którą naprawdę czuję, że muszę podkreślić, jest to, że ukryte i wyraźne rozwiązania rozwiązują te same problemy!, Pomyśl o tym nie jako o „różnych rozwiązaniach”, ale raczej jako o dwóch różnych sposobach rozwiązania tego samego problemu.

w wielu przypadkach można użyć zarówno domyślnego, jak i jawnego solvera, co spowoduje ten sam wynik. I myślę, że od tego powinniśmy zacząć!

jak działa analiza dynamiczna?

obie analizy rozwiązują problem, w którym szybkość rzeczy jest ważna. Oznacza to głównie, że obciążenie jest nakładane bardzo szybko. W takich przypadkach zawsze będziesz” powtarzał ” swój ładunek na czas., Zasadniczo wykorzystasz czas, aby powiedzieć solverowi „co się dzieje” i jak zmienia się obciążenie.

Po pierwsze, musisz określić, jak zmienia się obciążenie w czasie. Zwykle robisz to za pomocą wykresów, takich jak ten poniżej:

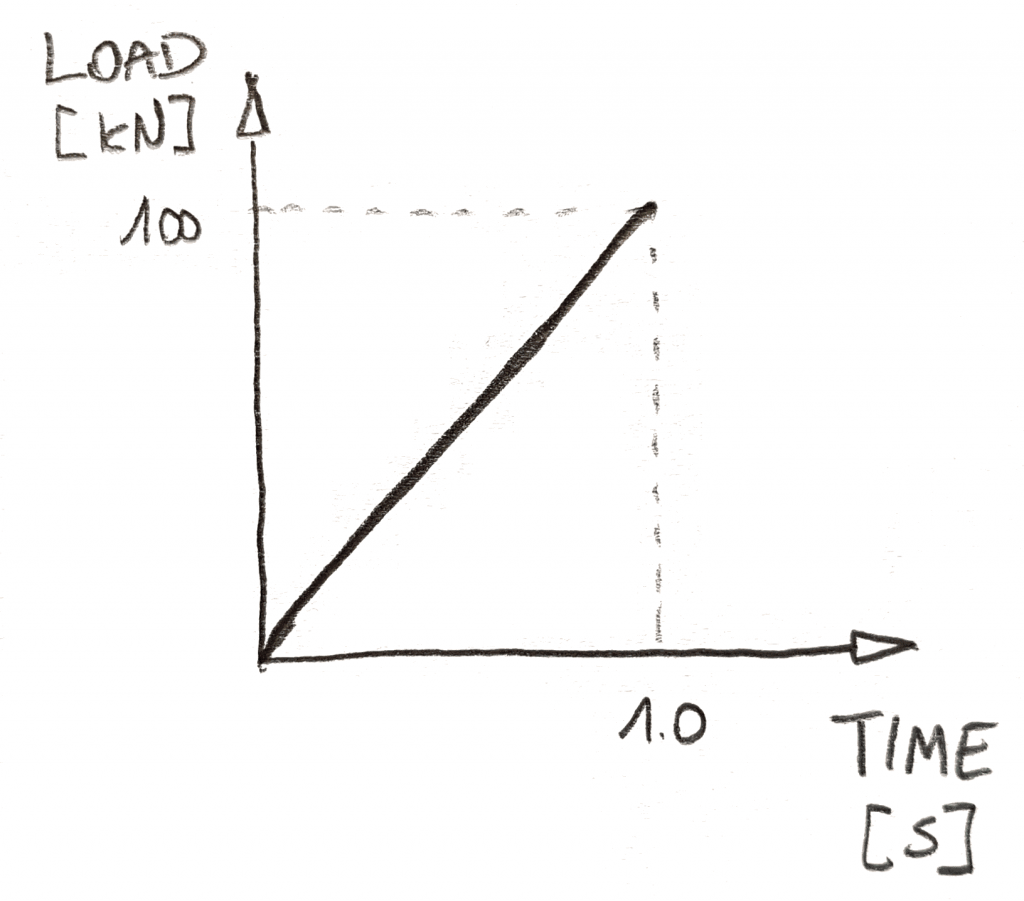
w nieliniowej analizie dynamicznej czas ma 2 role. Po pierwsze, pozwala powiedzieć solver, kiedy ile obciążenia należy zastosować. Po prostu musisz zaimplementować każde obciążenie za pomocą wykresu zależnego od czasu. Po drugie … czas to czas! Mówi rozwiązywaczowi, jak szybko wszystko idzie!,

wyobraź sobie, że chcesz mieć taką sekwencję ładowania:

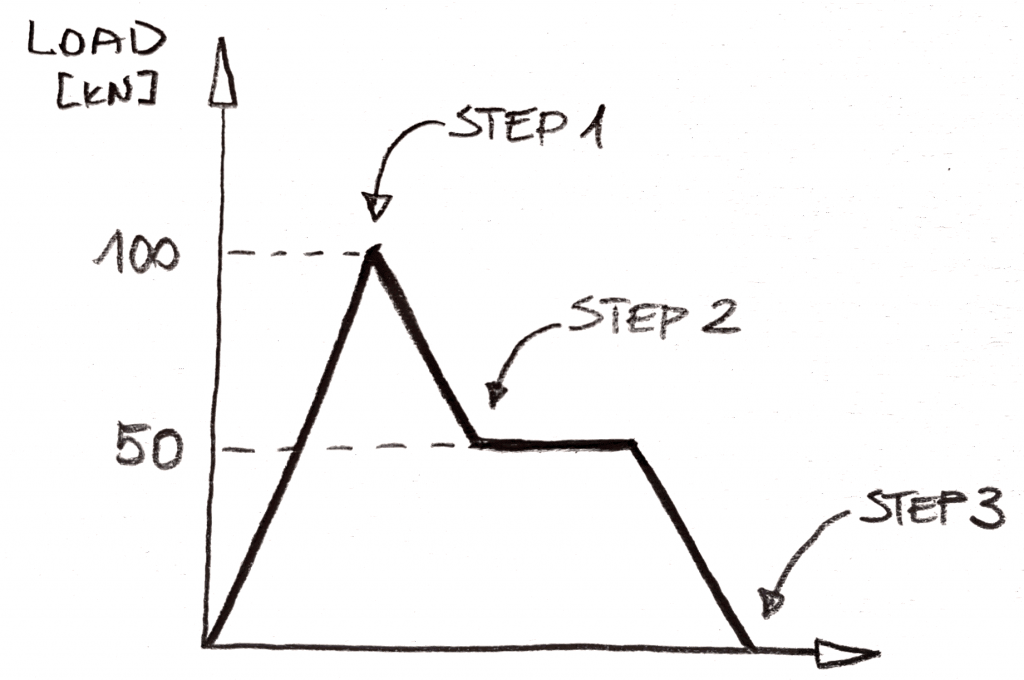
w static byłaby to analiza 3 „kroków” (w NX Nastran nazywane są podkasami, ale myślę, że Abaqus faktycznie użył „kroku” jako nazwy, ale nie pamiętam tego na pewno!). Pomysł byłby prosty, musisz zastosować 100kN obciążenia w kroku 1, a następnie usunąć 50KN obciążenia w Kroku 2 i usunąć 50KN w kroku 3. Nie ma możliwości włączenia „plateau” obciążenia po kroku 2 do analizy i zostanie ono pominięte., Logika jest prosta: brak zmian w obciążeniu = nic się nie zmienia w statycznym!

przyrost obciążenia statycznego

jeśli problem byłby bardzo nieliniowy, obciążenie byłoby „przyrostowe”. Rzadko można zastosować ” pełne obciążenie „do analizy nieliniowej przy”one go”! Zazwyczaj, solver będzie stosować tj. 1KN każdy „przyrost”. Oznacza to, że po 100 krokach zostanie zastosowane pełne obciążenie kroku 1. Ułatwia to rozwiązującemu uzyskanie poprawnej odpowiedzi.,

jako użytkownik możesz zdefiniować, jak duże przyrosty powinien używać solver. Istnieją również algorytmy modyfikujące przyrost obciążenia podczas analizy. Różne rozwiązania chcą, aby ustawić to w różny sposób. Zazwyczaj Pakiety FEA używają do tego mnożników obciążenia. Oznacza to, że można powiedzieć coś w stylu: „przy każdym przyroście zastosować dodatkowe 0.01 całego obciążenia”.

zajebiste… ale przejdźmy do dynamiki, dobrze?, W analizie dynamicznej można uzyskać rozkład obciążenia jak powyżej z taką definicją obciążenia:

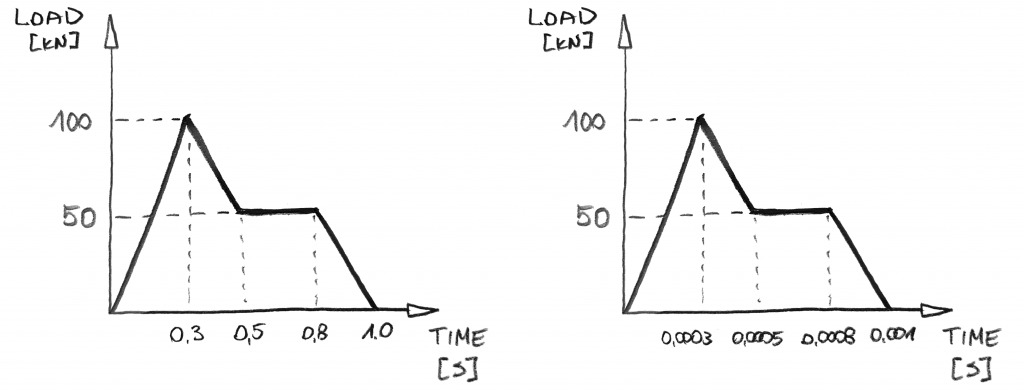
od razu można zauważyć kilka rzeczy:

• nie ma żadnych kroków! Dzieje się tak dlatego, że w analizie dynamicznej nie zwiększysz obciążenia. Będziesz zwiększyć czas! A ponieważ czas idzie ” stale „od zera do przepisanej wartości, możesz go zwiększyć w”jednym kroku”.

• czas jest najważniejszy! Jeśli chodzi o wartości obciążenia, powyższe wykresy są takie same., Ale to nie jest ten sam dynamiczny przypadek! Wykres po prawej stronie stosuje obciążenie 1000x szybciej! To nie jest coś, co można po prostu zignorować w analizie dynamicznej!

ogólnie rzecz biorąc, gdy chcesz rozwiązać problem dynamiczny, prosisz swojego solvera o zrobienie jednej rzeczy. Poproś go, aby obliczył szereg przyrostów czasu, aby zobaczyć, co dzieje się w modelu. W każdym z tych przyrostów czas nieznacznie wzrasta. To oczywiście zmienia również obciążenie w modelu. Dlatego musisz mieć Wykres zależny od czasu obciążenia., Tak więc solver „wie”, jakie obciążenie powinno być stosowane w którym czasie przyrostu. W tym zakresie działa tak samo jak przyrost obciążenia w analizie statycznej. Bonus jest, że ponieważ są inkrementacji czasu, efekty bezwładności mogą być brane pod uwagę, gdy rzeczy dzieją się wystarczająco szybko.

w tym zakresie zarówno analiza implicit jak i explicit robi mniej więcej to samo. Dzielą „czas analizy” na małe przyrosty, a następnie analizują, co dzieje się w twoim modelu jeden przyrost czasu po drugim. Ale tutaj kończą się podobieństwa!, Widzisz, istnieją różne podejścia do przyrostu Czasu, które możesz mieć!

Implicit vs Explicit-kiedy czas naprawdę ma znaczenie!

właśnie się nauczyłeś, że aby obliczyć nieliniowy problem dynamiczny, musisz stopniowo zwiększać „czas analizy”. Jak już wspomniałem, można to zrobić na dwa sposoby.

zacznę od podejścia implicit. Myślę, że jest to łatwiejsze do zrozumienia, ponieważ działa mniej więcej tak samo jak przyrost obciążenia w nieliniowej analizie statycznej!,

Jak działa Analiza Implicit:

Po pierwsze, implicit wydaje się być bardziej „podstawowym” rozwiązaniem. W istocie działa tak, jak myślisz, że powinno!

• po pierwsze, za każdym razem przyrostem ustalana jest „równowaga globalna” w modelu. Oznacza to, że każdy przyrost musi się zbiegać (dzieje się tak w iteracjach).

• po równowaga globalna jest ok, solver oblicza wszystkie lokalne zmienne elementów skończonych (naprężenia itp.) dla tego przyrostu.,

• korzyści: ponieważ globalna równowaga jest weryfikowana przy każdym przyroście czasowym, przyrosty te mogą być duże!
• wady: za każdym razem przyrost oblicza się powoli, ponieważ iteracje są potrzebne, aby uzyskać globalną równowagę.

Jeśli znasz nieliniową analizę statyczną, dzięki niejawnemu rozwiązywaniu poczujesz się „jak w domu”. Jako użytkownik zazwyczaj możesz powiedzieć, jak duży przyrost czasu chcesz mieć. To ogromna zaleta, którą łatwo przeoczyć., Ponieważ Explicit solver nie oferuje takiej możliwości!

rzućmy okiem na explicit incrementation next!

Jak działa Explicit Analysis:

ten jest funky. To działa w taki sposób, że nie musisz zbiegać się na każdym kroku! Nie ma kryteriów konwergencji do sprawdzenia i … żadnych iteracji! Zamiast sprawdzać „globalną równowagę” solver zakłada, że równowaga „po prostu istnieje”. Oznacza to, że solver przechodzi prosto do obliczania lokalnych zmiennych elementów skończonych!, Ponieważ taka procedura ma tylko jeden krok:

• Oblicz wszystkie lokalne zmienne elementów skończonych dla danego przyrostu i przejdź do następnego!

• korzyści: każdy przyrost oblicza się bardzo szybko!
• wady: aby to zadziałało, krok czasu musi być bardzo mały. W przeciwnym razie niemożliwe jest utrzymanie tej równowagi, która zakłada się, że „po prostu istnieje”. Aby to osiągnąć, użytkownik nie ma bezpośredniej kontroli nad tym, jak duże przyrosty czasu będzie przyjmować explicit solver., Sam Solver oblicza, jak małe czasy są nadal w porządku. A te dopuszczalne przyrosty czasu są bardzo małe! Dlatego wyraźne problemy powinny trwać ułamki sekundy! Gdyby trwały sekundy … potrzebowałbyś milionów przyrostów!

aby szybko podsumować: zarówno domyślne, jak i jawne rozwiązania rozwiązują te same rzeczy. Jedyna różnica polega na tym, jak te metody zwiększają czas.

technicznie rzecz biorąc, oba powinny dać taki sam wynik we wszystkich przypadkach., W końcu możesz przeanalizować ten sam problem z obydwoma podejściami. Oczywiście odpowiedź nie może zależeć od metody użytej do rozwiązania problemu! Ale oczywiście wybierzesz tylko jedno z podejść do następnego problemu, więc które? Przekonajmy się!

co jest dla Ciebie lepsze: jawne czy jawne?

uzgodniliśmy już, że możesz używać zarówno ukrytych, jak i jawnych rozwiązań do rozwiązywania tego samego typu problemów. Jedyną różnicą jest podejście do przyrostu czasu. Ale to nie jest trywialne!, Gdyby różnica była niewielka, nikt nie chciałby wdrożyć obu! Przyjrzyjmy się więc, jak Tym razem inkrementacja wpływa na rzeczy!

zarówno domyślne, jak i jawne rozwiązania mają pewne obszary, w których świecą. I jest nakładanie się w ich użyciu:

• ukryta analiza pozwala wybrać, jak duży powinien być przyrost czasu! Ten przyrost zajmie trochę czasu, aby obliczyć, ponieważ musi iterację dla globalnej równowagi najpierw. Ale możesz zrobić to „w miarę Duże” dla swojej analizy.,

• wyraźne przyrosty czasu obliczają się naprawdę szybko! Po prostu dlatego, że nie iterować dla globalnej równowagi… ale przyrost czasu nie jest Twój wybór! Solver po prostu zakłada, że” akceptowalny „przyrost czasu jest” X ” i idzie z nim. Zauważ, że to ” X ” może być z łatwością czymś w rodzaju 5e-7s … to jest super małe! Aby rozwiązać problem występujący w ciągu 1s, potrzebujesz 2 000 000 przyrostów!

• i tyle! Szybkość obliczeniowa jest dokładnie różnicą między implicit i explicit., Oczywiście wielkość jawnego kroku zależy od modelu, a czas obliczeniowy zależy od sprzętu. Istnieją jednak proste obserwacje, które możemy łatwo dokonać:

użyj implicit dla „powolnej analizy”!

jeśli to, co obliczasz, dzieje się w ciągu kilku sekund… nie ma sensu używać jawnego solvera. Przekopanie się przez miliony przyrostów czasu potrzebnych do obliczenia tego zajmie wieczność!, Zamiast tego Ustaw „rozsądny” krok czasowy dla analizy ukrytej (powiedzmy 100 równych przyrostów czasu dla analizy). Oczywiście, każdy z tych ukrytych przyrostów czasu będzie obliczany znacznie dłużej niż pojedynczy przyrost jawny. Ale nie dłużej niż setki tysięcy z nich!

użyj explicit do „szybkiej analizy”!

To oczywiste, prawda? Jeśli to, co obliczysz, dzieje się w małym ułamku sekundy, to twój przyjaciel., W ukrytej analizie, Twój przyrost czasu byłby bardzo mały … może nawet tak mały jak przyrost w wyraźnej analizie. W takim przypadku analiza explicit będzie przebiegać znacznie szybciej, ponieważ nie wymaga iteracji „global equilibrium”. Analiza implicit wymaga tych iteracji (niezależnie od kroku czasowego!).

Inbetween stuff!

oczywiście zdarzają się problemy, które zdarzają się w środku (np. uderzenie z prędkością 5m/s)., Zazwyczaj można rozwiązać taki problem z obu rozwiązujących, ale może to być denerwujące.

mam nadzieję, że pomoże Ci to dobrać odpowiednie podejście do Twoich problemów dynamicznych. Oczywiście, w końcu doświadczenie jest najlepszym przewodnikiem! Jeśli masz wątpliwości, Uruchom kilka typowych problemów zarówno w sposób niejawny, jak i jawny. W ten sposób będziesz mógł porównać wyniki (powinny być takie same). Ale co ważniejsze, będziesz mógł porównać czasy obliczeniowe! To da Ci możliwość sprawdzenia, co jest dla ciebie lepszym podejściem!,

jak jednoznacznie określić rozmiar kroku czasowego?

na razie wszystko ładnie i elegancko, ale myślę, że byłoby miło zająć się jednym dużym problemem. I to jest… jeśli nie wybierasz kroku czasowego w swojej wyraźnej analizie… to kto to robi?

matematyczne Wyjaśnienie wymagałoby omówienia maksymalnej częstotliwości naturalnej. Dzieje się tak, ponieważ maksymalny przyrost czasu „wciąż akceptowalny” jest odwrotnie proporcjonalny do maksymalnej częstotliwości naturalnej. Takie obliczenia można oczywiście wykonać., Wyniki zależą od siatki modelu (ile jest elementów itp.). Ale nie pójdziemy tam i są 2 powody: Po pierwsze, nie lubię matematyki (!). Po drugie, nie tak postępują w końcu solvers, mimo że jest to „właściwy sposób”.

solver może oczywiście obliczyć maksymalną częstotliwość naturalną, ale zajmuje to sporo czasu. A ponieważ musiałoby to być wykonane w każdym wyraźnym przyroście czasu (może być ich wiele!/ align = „left” / , Na szczęście istnieje sposób, aby ładnie oszacować tę wartość, analizując każdy element skończony w systemie oddzielnie! Fizyczna interpretacja tego oszacowania (powszechnie stosowana w rozwiązaniach) to:

maksymalny przyrost czasu w analizie jawnej:

przyrost czasu w analizie jawnej jest bardzo krótki. Jest to czas, w którym fala elastyczna (tj. fala uderzeniowa) może podróżować przez pojedynczy element skończony modelu. Oczywiście jest to weryfikowane dla wszystkich elementów skończonych w twoim modelu i wybierany jest najmniejszy czas.,

jak widać, istnieją 2 składniki do komponentu explicit time:

• elastyczna prędkość fali (aka prędkość dźwięku w Twoim materiale)! Zależy to tylko od materiału, który posiadasz w swoim modelu (i oczywiście różni się dla różnych materiałów!). Będziesz potrzebował modułu Young E, gęstości materiału i racji Poissona (w problemach 2D i 3D). Łatwo jest znaleźć tabele z listą prędkości fal elastycznych w różnych materiałach. Dla odniesienia w stali, jest to około 5200m/s (wiele metali jest około 4500-5500m / s).,

• Rozmiar elementu (i jakość)! Masz prędkość fali, ale to nie wystarczy! Aby poznać czas potrzebny na podróż przez element, musisz znać element „długość”. Podczas gdy jest to bardzo proste w elementach 1D (po prostu mają długość), staje się trudne w 2D i 3D. ta długość nie jest” po prostu ” najkrótszą krawędzią elementu, ponieważ elementy mogą mieć dość słabą geometrię. Są rzeczy, które solver robi, aby to obliczyć. W 2D może to być obszar elementu podzielony przez maksymalną długość krawędzi., W 3D może oznaczać, że objętość elementu jest podzielona przez maksymalną powierzchnię boczną. Dlatego nie tylko rozmiar elementu, ale także jakość elementów jest tak ważna w jednoznacznej analizie! W końcu … wszystko, czego potrzebujesz, to jeden słaby element, który naprawdę zaszkodzi Twojemu czasowi obliczeniowemu!

czytałem gdzieś, że chociaż powyższe jest „precyzyjnym” rozwiązaniem, solvery często używają „czynników bezpieczeństwa” na tym. Jeśli otrzymasz większy przyrost czasu niż elastyczna fala” ograniczenie prędkości ” błędy matematyczne wystąpić. Ponieważ stosowane są szacunki, rozwiązywacze często skracają czas „na wszelki wypadek”., Zazwyczaj współczynnik redukcji wynosi około 0,9, ale może się to oczywiście różnić w zależności od rozwiązania.

masowe skalowanie!

na koniec chciałbym coś szybko wspomnieć.

najprawdopodobniej zauważyłeś, że czas w explicit zależy tylko od siatki, modułu Younga i gęstości. Redukcja młodego modułu może oczywiście nie być idealna i często potrzebujesz małej siatki do analizy szczegółów. Ale w problemach „niskiej dynamiki” można spróbować zwiększyć wyraźny krok czasowy poprzez zwiększenie gęstości materiału.,

nazywa się to”skalowaniem masowym”. Pakiety FEA oferują nawet rozwiązania, w których gęstość wzrasta tylko w elementach, które „decydują” o przyroście czasu. Oznacza to, że czasami tylko małe porcje Twojego modelu stają się cięższe! W niektórych analizach można” uciec ” ze zwiększeniem masy modelu. W takim przypadku może to być rozwiązanie dla Ciebie. Pamiętaj, że to zmienia zachowanie Twojego modelu! Przy dużych przyspieszeniach należy zachować ostrożność!

podsumowanie

Nice!, Jesteś tutaj, dzięki za przeczytanie! Zakończmy to, aby było łatwiej zapamiętać!

• analiza dynamiczna obejmuje czas! Podczas stosowania obciążeń należy je zdefiniować w funkcji czasu. Często jest to relacja liniowa. Nie zmienia to jednak faktu, że istotną rolę odgrywa czas, w którym obciążenie jest nakładane (zwłaszcza jeśli ten czas jest krótki!).

• 2 smaki analizy dynamicznej! Możesz rozwiązać „rzeczywiste” problemy dynamiczne za pomocą ukrytych i jawnych algorytmów. Oba są w porządku i żaden z nich nie jest „lepszy”., Ale powinienem powiedzieć, że explicit solver jest częścią mniejszej liczby pakietów FEA. Ponieważ nie każdy pakiet FEA ma taki, jawny solver jest postrzegany jako” bardziej zaawansowany”.

• Ukryty solver jest naprawdę dobry, jeśli rzeczy w Twojej analizie dzieją się stosunkowo wolno. Załóżmy, że analiza jest dłuższa niż 1s bez żadnych nagłych rzeczy dzieje się w tym czasie. Zaletą jest to, że możesz wybrać, jak duży przyrost czasu chcesz. Nawet jeśli pojedynczy przyrost trwa dłużej, jest ich znacznie mniej!,

• explicit solver jest świetny do szybkich zdarzeń (powiedzmy szybszych niż 0.1 s). Tutaj nie możesz wybrać przyrostu czasu – solver ustawi go automatycznie. Chociaż są one zwykle bardzo małe, przynajmniej obliczają znacznie szybciej niż”Ukryte”. Explicit solver oblicza, jak duży powinien być przyrost czasu. Zależy to od szybkości dźwięku w Twoim materiale, minimalnego rozmiaru elementów skończonych(i jakości elementów!). W niektórych przypadkach można zmienić gęstość (nawet automatycznie tylko w „elementach decydujących”!), aby dostosować ten przyrost czasu., To działa, ponieważ szybkość dźwięku w Twoim materiale zależy od jego gęstości! Nazywa się to „skalowaniem masowym”.