Show Mobile Notice Show All Notes Hide All Notes
4-6. szakasz: egy gráf alakja, II. rész
az előző szakaszban láttuk, hogyan használhatjuk egy függvény első származékát, hogy információt kapjunk egy függvény grafikonjáról. Ebben a részben megnézzük azt az információt, amelyet egy függvény második származéka adhat nekünk egy függvény grafikonjáról.
mielőtt ezt megtesszük, szükségünk lesz néhány meghatározásra az útból. A fő koncepció, amelyet ebben a szakaszban tárgyalunk, a konkavitás. A konkavitást a legegyszerűbb grafikon segítségével látni (egy kicsit megadjuk a matematikai meghatározást).,
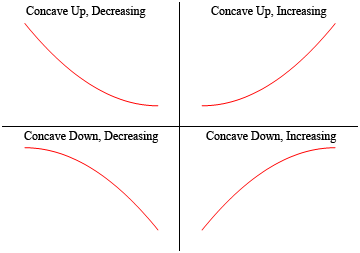
tehát egy függvény konkáv, ha” kinyílik”, és a függvény konkáv, ha” megnyit ” lefelé. Vegyük észre azt is, hogy a konkávságnak semmi köze a növekedéshez vagy csökkenéshez. A függvény lehet konkáv, vagy növekvő vagy csökkenő. Hasonlóképpen, egy függvény homorú lehet, vagy növekszik vagy csökken.
Ez valószínűleg nem a legjobb módja annak, hogy meghatározzuk a konkávságot azzal, hogy megmondjuk, hogy milyen módon “megnyílik”, mivel ez egy kissé homályos meghatározás. Itt van a konkavitás matematikai meghatározása.,
definíció 1
annak bizonyítására, hogy a fenti grafikonok valójában concavity állította fent itt a grafikon újra (felrobbantott egy kicsit, hogy a dolgok világosabbá).
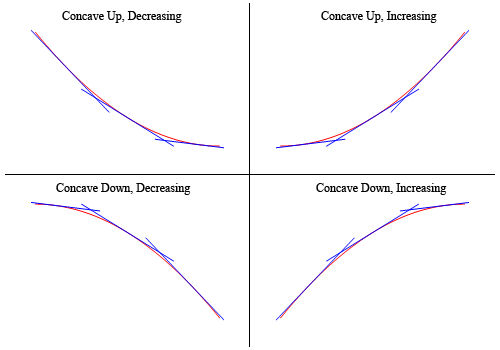
Tehát, mint látható, a két felső gráfban az összes rajzolt tangens vonal mind a függvény grafikonja alatt van, és ezek konkávok. Az alsó két gráfban az összes érintővonal a függvény gráfja felett van, ezek homorúak.,
ismét vegye figyelembe, hogy a konkávság és a funkció növekvő/csökkenő aspektusa teljesen különálló, és semmi köze egymáshoz. Ez azért fontos megjegyezni, mert a diákok gyakran összekeverik ezt a kettőt, és az egyikre vonatkozó információkat használják fel, hogy információt szerezzenek a másikról.
van még egy meghatározás, amelyet el kell hagynunk az útból.
Definition 2
a point \(x = c\) nevezzük inflexiós pont, ha a függvény folyamatos a ponton, és a konkávság a grafikon változik ezen a ponton.,
most, hogy az összes konkáv definíciónk van, ki kell hoznunk a második származékot a keverékbe. Végül is elkezdtük ezt a szakaszt, mondván, hogy a második származékot fogjuk használni, hogy információt szerezzünk a grafikonról. A következő tény egy függvény második származékát a konkávságához köti. Ennek bizonyítéka az extrák fejezet származékos Alkalmazások szakaszából származó igazolások.
tény
tehát ez a tény azt mondja nekünk, hogy az inflexiós pontok minden pont a második származékos változás jele., Az előző fejezetben láttuk, hogy egy függvény megváltoztathatja a jeleket, ha nulla vagy nem létezik. Vegye figyelembe, hogy az előző szakasz első származékával dolgoztunk, de az a tény, hogy egy függvény esetleg megváltoztatja a jeleket, ahol nulla vagy nem létezik, semmi köze az első származékhoz. Ez egyszerűen egy tény, amely minden funkcióra vonatkozik, függetlenül attól, hogy származékok-e vagy sem.,
Ez viszont azt mondja nekünk, hogy a lehetséges inflexiós pontok listája azok a pontok, ahol a második származék nulla vagy nem létezik, mivel ezek az egyetlen pontok, ahol a második származék megváltoztathatja a jelet.
vigyázzon azonban arra, hogy ne tegye azt a feltételezést, hogy csak azért, mert a második származék nulla vagy nem létezik, hogy a pont inflexiós pont lesz. Csak akkor tudjuk, hogy ez egy inflexiós pont, ha meghatározzuk a konkávságot mindkét oldalán. Csak akkor lesz inflexiós pont, ha a konkávság a pont mindkét oldalán eltérő.,
most, hogy tudjuk, concavity tudjuk használni ezt az információt, valamint a növekvő / csökkenő információkat az előző rész, hogy egy nagyon jó ötlet, hogy mi a grafikon kell kinéznie. Vessünk egy példát erre.
az előző példát egy másik módszer illusztrálására használhatjuk egy függvény egyes kritikus pontjainak relatív maximumokként vagy relatív minimumokként történő osztályozására.
amint egy kicsit látni fogjuk, nagyon óvatosnak kell lennünk a \(x = 0\)., Ebben az esetben a második származék nulla, de ez valójában nem jelenti azt, hogy \(x = 0\) nem relatív minimum vagy maximum. Majd meglátjuk néhány példa erre egy kicsit, de meg kell, hogy néhány más információt gondoskodott az első.
itt is fontos megjegyezni, hogy ebben a példában az összes kritikus pont olyan kritikus pont volt, amelyben az első származék nulla volt, és ez szükséges ahhoz, hogy ez működjön. Nem fogjuk tudni használni ezt a tesztet olyan kritikus pontokon, ahol a származék nem létezik.,
itt van a teszt, amely egy függvény néhány kritikus pontjának osztályozására használható. Ennek a tesztnek a bizonyítéka az extrák fejezet származékos Alkalmazások bizonyítékai részében található.
második származékos teszt
a második származtatott teszt harmadik része fontos észrevenni. Ha a második származék nulla, akkor a kritikus pont bármi lehet. Az alábbiakban három függvény grafikonjai láthatók, amelyek mindegyikének kritikus pontja \(x = 0\), az összes függvény második deriváltja nulla \(x = 0\), mégis mindhárom lehetőség ki van állítva.,
az első a \(f\bal( x \jobb) = {x^4}\) grafikonja. Ez a grafikon relatív minimuma \(x = 0\).
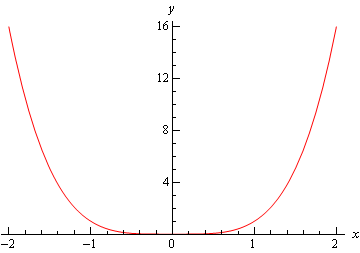
következő A \(F\bal( x \jobb) = – {x^4}\) grafikon, amelynek relatív maximális értéke \(x = 0\).

Végül itt van a \(f\left( x \right) = {x^3}\) grafikon, és ennek a grafikonnak sem relatív minimuma, sem relatív maximuma nem volt \(x = 0\).
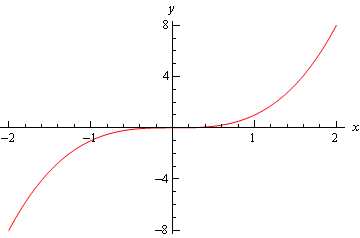
Tehát láthatjuk, hogy óvatosnak kell lennünk, ha a harmadik esetbe esünk., Azokban az időkben, amikor ebbe az ügybe esünk, más módszereket kell alkalmaznunk a kritikus pont osztályozására. Ez általában az első származékos teszttel történik.
menjünk vissza, és vessünk egy pillantást az első példa kritikus pontjaira, és használjuk a második származékos tesztet, ha lehetséges.
dolgozzunk még egy példát.















