Mostra avviso mobile Mostra tutte le note Nascondi tutte le note
Sezione 4-6 : La forma di un grafico, Parte II
Nella sezione precedente abbiamo visto come potremmo usare la derivata prima di una funzione per ottenere alcune informazioni sul grafico di una funzione. In questa sezione esamineremo le informazioni che la derivata seconda di una funzione può darci sul grafico di una funzione.
Prima di farlo avremo bisogno di un paio di definizioni fuori strada. Il concetto principale di cui parleremo in questa sezione è la concavità. La concavità è più facile da vedere con un grafico (daremo la definizione matematica in un po’).,
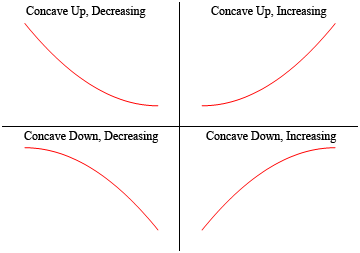
Quindi, una funzione è concava se “si apre” e la funzione è concava se “si apre”. Si noti anche che la concavità non ha nulla a che fare con l’aumento o la diminuzione. Una funzione può essere concava e aumentare o diminuire. Allo stesso modo, una funzione può essere concava verso il basso e aumentare o diminuire.
Probabilmente non è il modo migliore per definire la concavità dicendo in che modo “si apre” poiché questa è una definizione un po’ nebulosa. Ecco la definizione matematica di concavità.,
Definizione 1
Per mostrare che i grafici sopra hanno in effetti la concavità rivendicata sopra, ecco di nuovo il grafico (fatto saltare un po ‘ per rendere le cose più chiare).
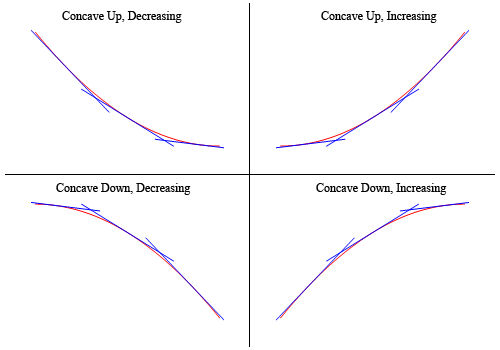
Quindi, come puoi vedere, nei due grafici superiori tutte le linee tangenti disegnate sono tutte sotto il grafico della funzione e queste sono concave. Nei due grafici inferiori tutte le linee tangenti sono sopra il grafico della funzione e queste sono concave verso il basso.,
Ancora una volta, si noti che la concavità e l’aspetto crescente / decrescente della funzione sono completamente separati e non hanno nulla a che fare l’uno con l’altro. Questo è importante notare perché gli studenti spesso mescolano questi due e utilizzano le informazioni su uno per ottenere informazioni sull’altro.
C’è un’altra definizione che dobbiamo toglierci di mezzo.
Definizione 2
Un punto \(x = c\) è chiamato punto di flesso se la funzione è continua nel punto e la concavità del grafico cambia in quel punto.,
Ora che abbiamo tutte le definizioni di concavità fuori strada abbiamo bisogno di portare la derivata seconda nel mix. Dopo tutto abbiamo iniziato questa sezione dicendo che avremmo usato la seconda derivata per ottenere informazioni sul grafico. Il fatto seguente collega la derivata seconda di una funzione alla sua concavità. La prova di questo fatto è nella sezione Prove da applicazioni derivate del capitolo Extra.
Fact
Quindi, ciò che questo fatto ci dice è che i punti di inflessione saranno tutti i punti erano il segno delle modifiche derivate seconde., Abbiamo visto nel capitolo precedente che una funzione può cambiare segni se è zero o non esiste. Si noti che stavamo lavorando con la derivata prima nella sezione precedente, ma il fatto che una funzione possa cambiare i segni dove è zero o non esiste non ha nulla a che fare con la derivata prima. È semplicemente un fatto che si applica a tutte le funzioni indipendentemente dal fatto che siano derivate o meno.,
Questo a sua volta ci dice che un elenco di possibili punti di inflessione saranno quei punti in cui la derivata seconda è zero o non esiste, poiché questi sono gli unici punti in cui la derivata seconda potrebbe cambiare segno.
Fai attenzione tuttavia a non ipotizzare che solo perché la derivata seconda è zero o non esiste che il punto sarà un punto di flesso. Sapremo solo che è un punto di flesso una volta che determineremo la concavità su entrambi i lati di esso. Sarà solo un punto di flesso se la concavità è diversa su entrambi i lati del punto.,
Ora che conosciamo la concavità possiamo usare queste informazioni così come le informazioni crescenti/decrescenti della sezione precedente per avere una buona idea di come dovrebbe essere un grafico. Diamo un’occhiata a un esempio di questo.
Possiamo usare l’esempio precedente per illustrare un altro modo per classificare alcuni dei punti critici di una funzione come massimi relativi o minimi relativi.
Come vedremo tra un po ‘ dovremo stare molto attenti con \(x = 0\)., In questo caso la derivata seconda è zero, ma ciò non significa che \(x = 0\) non sia un minimo o un massimo relativo. Vedremo alcuni esempi di questo in un po’, ma abbiamo bisogno di ottenere alcune altre informazioni curato prima.
È anche importante notare che tutti i punti critici in questo esempio erano punti critici in cui la derivata prima era zero e questo è necessario perché funzioni. Non saremo in grado di utilizzare questo test su punti critici in cui la derivata non esiste.,
Ecco il test che può essere utilizzato per classificare alcuni dei punti critici di una funzione. La prova di questo test è nella sezione Prove di applicazioni derivate del capitolo Extra.
Test della derivata seconda
La terza parte del test della derivata seconda è importante da notare. Se la derivata seconda è zero, il punto critico può essere qualsiasi cosa. Di seguito sono riportati i grafici di tre funzioni che hanno tutte un punto critico a \(x = 0\), la derivata seconda di tutte le funzioni è zero a \(x = 0\) e tuttavia tutte e tre le possibilità sono esposte.,
Il primo è il grafico di \(f\left( x \right) = {x^4}\). Questo grafico ha un minimo relativo a \(x = 0\).
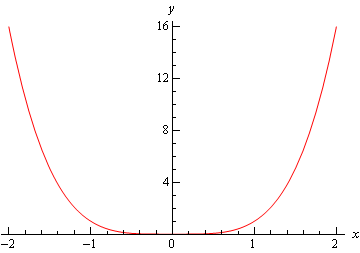
Il prossimo è il grafico di \(f\left( x \right) = – {x^4}\) che ha un massimo relativo a \(x = 0\).

Infine, c’è il grafico di \(f\left( x \right) = {x^3}\) e questo grafico non ha né un minimo relativo né un massimo relativo a \(x = 0\).
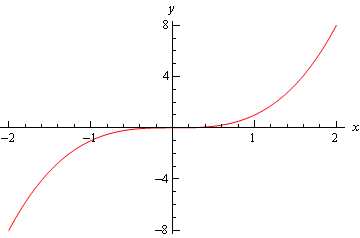
Quindi, possiamo vedere che dobbiamo stare attenti se cadiamo nel terzo caso., Per quei tempi in cui cadiamo in questo caso dovremo ricorrere ad altri metodi per classificare il punto critico. Questo di solito viene fatto con il primo test derivato.
Torniamo indietro e diamo un’occhiata ai punti critici del primo esempio e usiamo il Secondo Test Derivato su di essi, se possibile.
Facciamo un altro esempio.















