afișare anunț mobil afișează toate notele ascunde toate notele
Section 4-6: The Shape of a Graph, Part II
în secțiunea anterioară am văzut cum am putea folosi prima derivată a unei funcții pentru a obține informații despre graficul unei funcții. În această secțiune vom analiza informațiile pe care al doilea derivat al unei funcții ne poate da o despre graficul unei funcții.înainte de a face acest lucru, vom avea nevoie de câteva definiții din drum. Conceptul principal pe care îl vom discuta în această secțiune este concavitatea. Concavitatea este mai ușor de văzut cu un grafic (vom da definiția matematică într-un pic).,
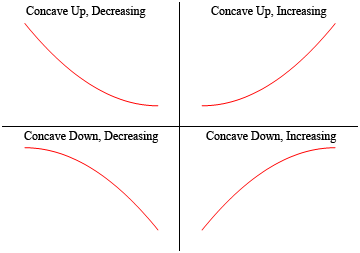
deci, o funcție este concavă în sus dacă „se deschide” în sus și funcția este concavă în jos dacă „se deschide” în jos. Observați, de asemenea, că concavitatea nu are nimic de-a face cu creșterea sau scăderea. O funcție poate fi concavă în sus și fie în creștere, fie în scădere. În mod similar, o funcție poate fi concavă în jos și fie în creștere, fie în scădere.probabil că nu este cel mai bun mod de a defini concavitatea spunând în ce mod „se deschide”, deoarece aceasta este o definiție oarecum nebuloasă. Iată definiția matematică a concavității.,
definiția 1
pentru a arăta că graficele de mai sus au, de fapt, concavitatea revendicată mai sus, aici este din nou graficul (aruncat puțin pentru a face lucrurile mai clare).deci, după cum puteți vedea, în cele două grafice superioare toate liniile tangente schițate sunt toate sub graficul funcției și acestea sunt concave în sus. În cele două grafice inferioare, toate liniile tangente sunt deasupra graficului funcției și acestea sunt concave în jos.,din nou, observați că concavitatea și aspectul crescător / descrescător al funcției sunt complet separate și nu au nimic de-a face unul cu celălalt. Acest lucru este important de reținut, deoarece elevii amestecă adesea aceste două și folosesc informații despre unul pentru a obține informații despre celălalt.
există încă o definiție pe care trebuie să o dăm la o parte.
definiția 2
un punct \(x = c\) se numește punct de inflexiune dacă funcția este continuă în punct și concavitatea graficului se schimbă în acel punct.,acum, că avem toate definițiile de concavitate din modul în care trebuie să aducem al doilea derivat în amestec. După toate, am început această secțiune spunând că vom folosi al doilea derivat pentru a obține informații despre Grafic. Următorul fapt se referă la al doilea derivat al unei funcții la concavitatea sa. Dovada acestui fapt se află în secțiunea Proofs From Derivative Applications din capitolul Extras.deci, ceea ce ne spune acest fapt este că punctele de inflexiune vor fi toate punctele au fost al doilea semn de modificări derivate., Am văzut în capitolul precedent că o funcție poate schimba semnele dacă este zero sau nu există. Rețineți că am fost de lucru cu primul derivat din secțiunea anterioară, dar faptul că o funcție, eventual, schimbarea semne în cazul în care este zero sau nu există nu are nimic de-a face cu primul derivat. Este pur și simplu un fapt care se aplică tuturor funcțiilor, indiferent dacă sunt derivate sau nu.,la rândul său, aceasta ne spune că o listă de posibile puncte de inflexiune vor fi acele puncte în care al doilea derivat este zero sau nu există, deoarece acestea sunt singurele puncte în care al doilea derivat ar putea schimba semnul.cu toate acestea, aveți grijă să nu presupuneți că doar pentru că al doilea derivat este zero sau nu există, punctul va fi un punct de inflexiune. Vom ști doar că este un punct de inflexiune odată ce determinăm concavitatea de ambele părți ale acesteia. Va fi doar un punct de inflexiune dacă concavitatea este diferită pe ambele părți ale punctului.,
acum că știm despre concavitate, putem folosi aceste informații, precum și informațiile în creștere/scădere din secțiunea anterioară pentru a obține o idee destul de bună despre cum ar trebui să arate un grafic. Să aruncăm o privire la un exemplu în acest sens.putem folosi exemplul anterior pentru a ilustra un alt mod de a clasifica unele dintre punctele critice ale unei funcții ca maxime relative sau minime relative.
după cum vom vedea într-un pic, va trebui să fim foarte atenți cu \(x = 0\)., În acest caz, al doilea derivat este zero, dar asta nu va însemna de fapt că \(x = 0\) nu este un minim sau maxim relativ. Vom vedea câteva exemple în acest sens într-un pic, dar trebuie să ne ocupăm mai întâi de alte informații.de asemenea, este important să rețineți că toate punctele critice din acest exemplu au fost puncte critice în care primul derivat a fost zero și acest lucru este necesar pentru ca acesta să funcționeze. Nu vom putea folosi acest test pe puncte critice în care derivatul nu există.,
aici este testul care poate fi folosit pentru a clasifica unele dintre punctele critice ale unei funcții. Dovada acestui test se află în secțiunea Proofs of Derivative Applications din capitolul Extras.
al doilea test derivat
a treia parte a celui de-al doilea test derivat este important de observat. Dacă al doilea derivat este zero, atunci punctul critic poate fi orice. Mai jos sunt graficele a trei funcții, toate având un punct critic la \(x = 0\), Al doilea derivat al tuturor funcțiilor este zero la \(x = 0\) și totuși toate cele trei posibilități sunt expuse.,
primul este graficul lui \(f \ left (x \right) = {x^4}\). Acest grafic are un minim relativ la \(x = 0\).
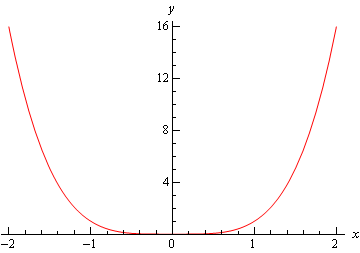
următorul este graficul \(F\left( x \right) = – {x^4}\) care are un maxim relativ la \(x = 0\).

în cele din Urmă, există graficul \(f\left( x \right) = {x^3}\) și acest grafic avut nici o rudă minim sau o relativă maximă la \(x = 0\).
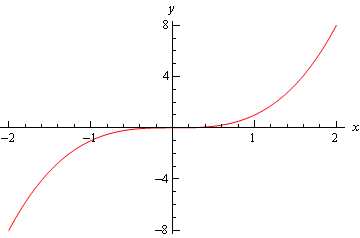
deci, putem vedea că trebuie să fim atenți dacă intrăm în al treilea caz., Pentru acele momente în care intrăm în acest caz, va trebui să recurgem la alte metode de clasificare a punctului critic. Acest lucru se face de obicei cu primul test derivat.să ne întoarcem și să aruncăm o privire asupra punctelor critice din primul exemplu și să folosim al doilea test derivat pe ele, dacă este posibil.
să lucrăm încă un exemplu.















