モバイル通知を表示すべてのノートを表示すべてのノートを非表示
セクション4-6:グラフの形状、パートII
前のセクションでは、関数の一次導関数を使用して関数のグラフに関する情報を取得する方法を見ました。 このセクションでは、関数の二次導関数が関数のグラフについて私たちに与えることができる情報を見ていきます。
これを行う前に、いくつかの定義が必要になります。 このセクションで議論する主なコンセプトは凹部です。 凹部はグラフで見るのが最も簡単です(数学的定義を少し説明します)。,
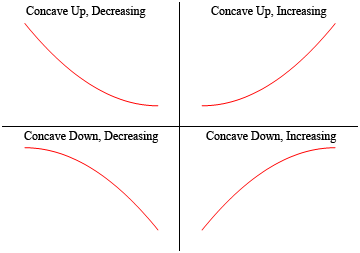
したがって、関数は”開く”場合は凹状になり、”開く”場合は凹状になります。 凹部は増加または減少とは何の関係もないことにも注意してください。 関数は、増加または減少のいずれかに凹状にすることができます。 同様に、関数は凹状になり、増加または減少のいずれかになります。
これはやや漠然とした定義であるため、どちらの方法で”開く”かを言って凹みを定義する最良の方法ではないでしょう。 ここに凹みの数学的定義があります。,
定義1
上記のグラフが実際には上で主張されている凹みを持っていることを示すために、ここで再びグラフがあります(物事をより明確にす
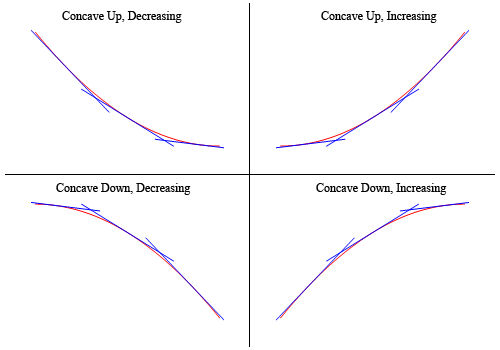
だから、あなたが見ることができるように、二つの上のグラフでは、スケッチされた接線のすべてはすべて関数のグラフの下にあり、これらは 下の二つのグラフでは、すべての接線は関数のグラフの上にあり、これらは凹状です。,
繰り返しますが、関数の凹みと増減の側面は完全に分離されており、お互いに何の関係もありません。 学生はしばしばこれら二つを混在させ、一方についての情報を使用して他方についての情報を取得するために注意することが重要です。
邪魔にならないようにするためにもう一つ定義があります。
定義2
点\(x=c\)は、関数がその点で連続であり、その点でグラフの凹部が変化する場合、変曲点と呼ばれます。,
すべての凹みの定義ができたので、二次導関数をミックスに入れる必要があります。 このセクションでは、グラフに関する情報を取得するために二次導関数を使用すると言って、このセクションから始めました。 次の事実は、関数の二次導関数をその凹部に関連付ける。 この事実の証明は、Extrasの章のDerivative Applicationsからの証明セクションにあります。
事実
だから、この事実が私たちに伝えることは、変曲点がすべての点になるということです二次導関数の変化記号でした。, 前の章では、関数がゼロであるか存在しない場合、関数が符号を変更する可能性があることを見ました。 前のセクションでは一次導関数を使用していましたが、関数がゼロまたは存在しない符号を変更する可能性があるという事実は、一次導関数とは それは単に、それらが導関数であるかどうかにかかわらず、すべての関数に適用される事実です。,
これは、二次導関数が符号を変える可能性のある唯一の点であるため、二次導関数がゼロであるか存在しない可能性のある変曲点のリストがそれらの点になることを示しています。
ただし、二次導関数がゼロであるか、または存在しないという理由だけで、その点が変曲点になるという仮定をしないように注意してください。 我々はそれの両側の凹部を決定したら、それが変曲点であることを知っているだけでしょう。 点の両側で凹部が異なる場合にのみ変曲点になります。,
凹部について知ったので、この情報と前のセクションの増減情報を使用して、グラフがどのように見えるかをかなり良く知ることができます。 その例を見てみましょう。
前の例を使用して、関数の臨界点のいくつかを相対最大値または相対最小値として分類する別の方法を示すことができます。
少しでわかるように、\(x=0\)に非常に注意する必要があります。, この場合、二次導関数はゼロですが、実際には\(x=0\)が相対的な最小値または最大値ではないことを意味するものではありません。 これのいくつかの例を少し見てみましょうが、まず他の情報を処理する必要があります。
この例の臨界点はすべて一次導関数がゼロである臨界点であり、これが機能するためにはこれが必要であることに注意することも重要です。 導関数が存在しない臨界点では、この検定を使用することはできません。,
ここでは、関数の臨界点のいくつかを分類するために使用できるテストです。 このテストの証明は、Extrasの章のProofs of Derivative Applicationsセクションにあります。
二次導関数テスト
二次導関数テストの第三の部分は、注意することが重要です。 二次導関数がゼロの場合、臨界点は何でもかまいません。 以下は、すべて\(x=0\)に臨界点を持ち、すべての関数の二次導関数は\(x=0\)においてゼロであり、三つの可能性はすべて示されている三つの関数のグラフ,最初は\(f\left(x\right)={x^4}\)のグラフです。 このグラフは\(x=0\)で相対的な最小値を持ちます。
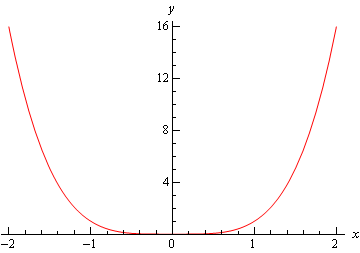
次は、\(f\left(x\right)=-{x^4}\)のグラフであり、これは\(x=0\)で相対的に最大値を持ちます。

最後に、\(f\left(x\right)={x^3}\)のグラフがあり、このグラフは\(x=0\)で相対最小値または相対最大値を持っていませんでした。
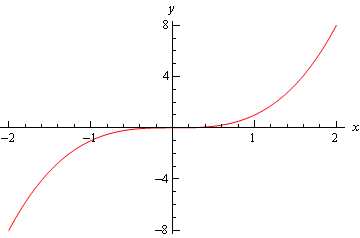
だから、私たちは第三のケースに分類される場合、我々は注意する必要があることがわかります。, 私たちがこのケースに陥ったときには、臨界点を分類する他の方法に頼らなければなりません。 これは通常、一次微分検定で行われます。
戻って最初の例の臨界点を見て、可能であればそれらに二次導関数テストを使用しましょう。
もう一つの例を考えてみましょう。















