쇼 모바일 통지를 보여 모든 노트 모든 노트 숨기기
섹션 4-6:의 형태 그래프,파트 II
이전 섹션에서 우리가 보았다 어떻게 우리가 사용할 수 있는 첫 번째 유도체의 함수에 대 한 몇 가지 정보를 얻을 그래프의 기능입니다. 이 섹션에서는 함수의 두 번째 파생어가 함수의 그래프에 대해 우리에게 줄 수있는 정보를 살펴 보겠습니다.이 작업을 수행하기 전에 몇 가지 정의가 필요합니다. 이 섹션에서 논의 할 주요 개념은 오목입니다. Concavity 는 그래프로 보는 것이 가장 쉽습니다(수학적 정의를 조금씩 알려 드리겠습니다).,
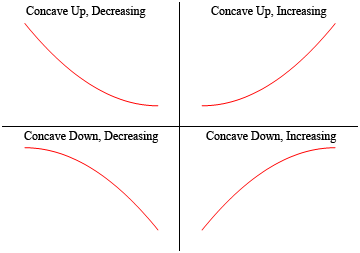
도,함수의 오목한다면 그것은”열”고 기능은 오목한다면 아래로”열”니다. 오목성이 증가하거나 감소하는 것과는 아무 상관이 없다는 것뿐만 아니라 주목하십시오. 기능은 오목 위로 증가하거나 감소 할 수 있습니다. 마찬가지로 함수가 아래로 오목 할 수 있으며 증가 또는 감소 할 수 있습니다.
그것은 아마 최고의 정의하는 방법은 오목으로 말하는”여기 때문에”이는 다소 애매한 정의입니다. 여기 concavity 의 수학적 정의가 있습니다.,
Definition1
를 표시하는 그래프 위의 사실이 오목을 주장 위에 여기 그래프 다시(불어진 작은 것을 명확하).
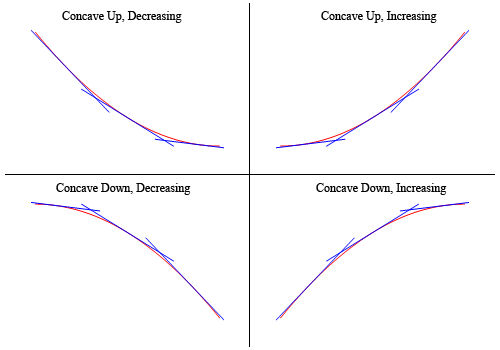
그래서,당신이 볼 수 있듯이,에서 두쪽 그래프는 모든 접선 스케치에서는 모든 아래 그래프의 기능과 이들은 오목한다. 아래 두 그래프에서 모든 접선 선은 함수의 그래프 위에 있으며 이들은 아래로 오목합니다.,
보시다시피는 오목 및 증가/감소 면의 기능이 완전히 분리하고 아무것도하지 않을 수행됩니다. 이것은 중요하기 때문에 학생들이 자주 섞는 이러한 두 가지고 사용 중 하나에 대한 자세한 정보에 대한 정보를 얻을 수 있다.
우리가 길에서 벗어나야 할 정의가 하나 더 있습니다.
정의 2
A 지점\(x=c\)라는 변곡점의 경우 함수가 지속적인 시점에서 그리고 오목의 변화 그래프에서는 점이다.,이제 우리는 두 번째 파생물을 믹스에 가져 오는 데 필요한 모든 concavity 정의를 가지고 있습니다. 우리 후의 모든 시작 이 섹션에서 말하는 우리가 사용하게 될 것 두 번째는 파생 상품에 대한 정보를 얻을 수 있습니다. 다음 사실은 함수의 두 번째 파생어를 그 오목 성과 관련시킵니다. 이 사실의 증거는 Extras 장의 파생 응용 프로그램에서 증명 섹션에 있습니다.
사실
이렇게,무엇이 사실이 우리들에게 말하는 변곡인의 모든 지점이 두 번째는 파생물의 변경 등록하십시오., 우리는 이전 장에서 함수가 0 이거나 존재하지 않는 경우 부호를 변경할 수 있음을 보았습니다. 참고로 우리와 함께 작업을 했는 첫 번째 파생은 이전 섹션에서만 사는 기능을 가능성이 변화하는 징후가 어디에나 존재하지 않는 함께 할 수 없는 첫 번째 유도체. 단순히 파생 상품인지 여부에 관계없이 모든 기능에 적용되는 사실입니다.,
이 설정에서는 목록이 가능한 변곡점이 될 것입니다 그 점을 어디에 두 번째는 파생상품이나 존재하지 않으로,이러한 유일한 포인트는 두 번째 파생을 변경할 수 있 등록하십시오.그러나 두 번째 파생어가 0 이거나 존재하지 않는다고해서 그 점이 변곡점이 될 것이라는 가정을하지 않도록주의하십시오. 우리는 일단 우리가 그것의 양쪽에 오목성을 결정하면 그것이 변곡점이라는 것을 알게 될 것입니다. 점의 양쪽에서 오목점이 다른 경우에만 변곡점이됩니다.,
이제는 우리가 알고 있는 오목한 우리는 이 정보를 사용할 수 있으로 증가/감소한 정보를 이전 섹션은 매우 좋은 아이디어가 무엇인지의 그래프는 다음과 같이 보일 것입니다. 그 예를 살펴 보겠습니다.앞의 예제를 사용하여 함수의 임계점 중 일부를 상대 최대 값 또는 상대 최소값으로 분류하는 또 다른 방법을 설명 할 수 있습니다.
우리가 조금에서 볼 수 있듯이\(x=0\)에 매우주의해야합니다., 이 경우 두 번째 파생어는 0 이지만 실제로\(x=0\)가 상대 최소 또는 최대 값이 아님을 의미하지는 않습니다. 우리는 이것에 대한 몇 가지 예를 조금씩 보게 될 것이지만,먼저 다른 정보를 알아야합니다.
그것은 또한 중요하다고 여기에는 모든 중요한 포인트에 이를 들어 있었다 중요한 포인트에서는 처음 파생했 제 이름이 필요합니다. 우리는 파생물이 존재하지 않는 임계점에서이 테스트를 사용할 수 없을 것입니다.,다음은 함수의 임계점 중 일부를 분류하는 데 사용할 수있는 테스트입니다. 이 테스트의 증명은 Extras 장의 파생 응용 프로그램 증명 섹션에 있습니다.
두 번째 파생 테스트
두 번째 파생 테스트의 세 번째 부분은 알아 두는 것이 중요합니다. 두 번째 파생어가 0 이면 임계점은 무엇이든 될 수 있습니다. 아래의 그래프를 세 가지 기능을 가지고 모두가 중요한 포인트에서\(x=0\),두 번째 유도체의 모든 기능을 제\(x=0\)며,아직 세 개의 모든 가능성을 전시하고 있습니다.,
첫 번째는\(f\left(x\right)={x^4}\)의 그래프입니다. 이 그래프는\(x=0\)에서 상대적 최소값을가집니다.
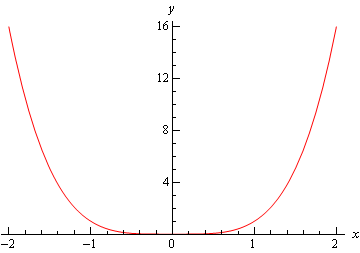
다음은\(x=0\)에서 상대 최대 값을 갖는\(f\left(x\right)=-{x^4}\)의 그래프입니다.

마지막으로,그래프의\(f\left(x\오른쪽)={x^3}\)이 그래프도 상대적인 최소한 또는 상대에서 최대\(x=0\).세 번째 경우에 빠지면 조심해야한다는 것을 알 수 있습니다., 우리가이 사건에 빠질 때 그 시간을 위해 우리는 임계점을 분류하는 다른 방법에 의지해야 할 것입니다. 이것은 일반적으로 첫 번째 파생 테스트로 수행됩니다.
돌아가서 첫 번째 예에서 중요한 점을 살펴보고 가능한 경우 두 번째 파생 테스트를 사용하십시오.
한 가지 더 예를 들어 보겠습니다.















