Good Mood

Bilde dette: Du gjør en presentasjon av Ph. D. avhandling om stabilitet på et av seminarene. Alt går greit, og til slutt, det er spørsmålet tid! Og noen ut av det blå spør: «hva er forskjellen mellom implisitt og eksplisitt tilnærming?»! Og siden du gjør statisk stabilitet… du aldri har hørt disse vilkår! Ja… er det gjort det!, Nå er jeg litt klokere, så la oss ta en nærmere titt på forskjellene mellom Implisitt og Eksplisitt analyse

Implisitt og Eksplisitt analyse ulik tilnærming til tid incrementation. I Implisitt analyse hver gang tilvekst har å konvergere, men du kan stille ganske lenge om gangen. Eksplisitt på den annen side trenger ikke å møtes hvert inkrement, men for løsningen å være nøyaktig tid intervaller må være super liten.

Dette høres ganske enkelt ut, ikke sant?, Med mindre du begynner å tenke på ting som «som en bør jeg bruke» eller «hvor liten skal den eksplisitte tidsintervallet være», og ting som det. Ingen bekymringer, jeg har det du trenger!

La oss dykke ned i!

Dynamics på sitt beste – Implisitt/Eksplisitt!

Du vil bruke Implisitt og Eksplisitt solvers å løse dynamiske problemer. Dette betyr at du ikke trenger å vite slike ting hvis du gjør statisk analyse., Hvis du er usikker på forskjellen mellom statisk og dynamisk analyse, vennligst les dette innlegget først – det vil gjøre ting lettere å forstå!

Dynamisk analyse i et nøtteskall:

Dynamisk analyse løser problemer med treghet effekter. De vises, når ting endres raskt i modellen (raskt påføres belastninger, slag, etc.). Ingeniører vanligvis reffer til dette som «ikke-lineære dynamiske».

Det bør bemerkes, som ofte ingeniører ringe andre analyser «dynamisk», så vel., Ting som Modal analyse eller Tvungen Respons analyse som tilbyr med vibrasjoner. Noen ganger er de som er kalt «lineær dynamisk», men det er vanligvis en god idé å sørge for at hva man mener når de bruker slike uttrykk. Mens «lineære dynamiske» problemer er virkelig interessant, jeg vil ikke diskutere dem her. Du kan lære mer om dem lese dette innlegget!

Det første jeg virkelig føler jeg har å understreke er at implisitte og eksplisitte solvers løse DE SAMME problemene!, Tenk om den ikke er så «annerledes solvers», men heller som to ulike måter å løse det samme problemet.

I mange tilfeller kan du bruke både implisitt og eksplisitt solver, og de vil gi det samme resultatet. Og jeg tror det er der vi må begynne!

Hvordan dynamisk analyse fungerer?

Både av analysen er å løse et problem der hastigheten av ting som er viktig. Dette for det meste betyr at lasten er brukt veldig fort. I slike tilfeller, vil du alltid «gjenta» last i tid., I utgangspunktet, du vil vil bruke tid på å fortelle solver «hva skjer» og hvordan belastningen er i endring.

for det Første, du har til å definere hvordan legg endrer seg i tid. Du vanligvis gjøre dette ved hjelp av diagrammer, som vist nedenfor:

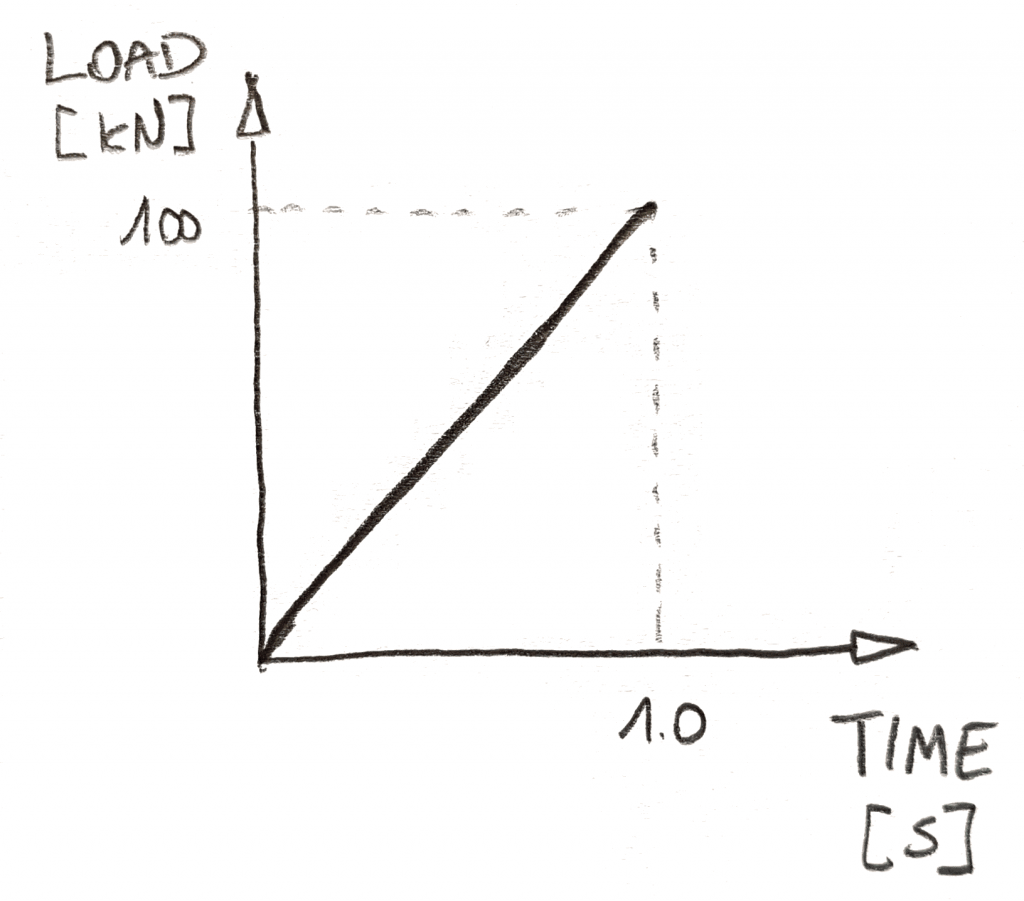
I ikkelineære dynamiske analyser, tiden har 2 roller. For det første, det kan du fortelle solver, når hvor mye belastning bør være anvendt. Du bare nødt til å gjennomføre hver belastning med en gang avhengige av diagrammet. For det andre… tid er tid! Det forteller brukeren hvor fort ting går!,

Tenk deg at du ønsker å ha en slik belastning rekkefølge:

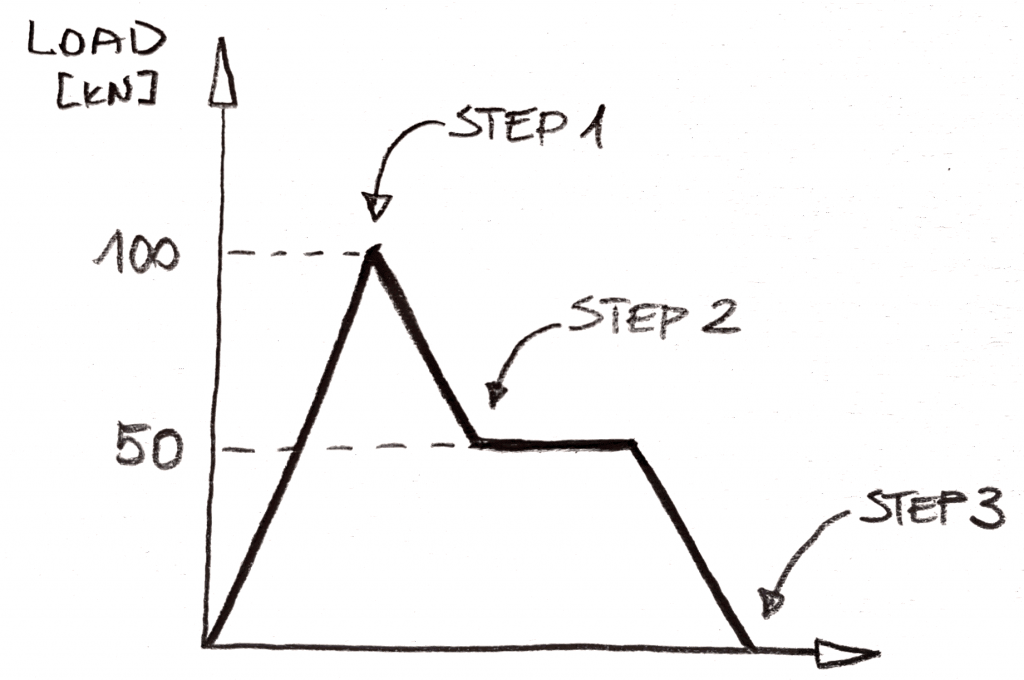
I statisk dette ville være en 3 «steg» analyse (de som er kalt subcases i NX Nastran, men jeg tror Abaqus som faktisk brukes i «trinn» som et navn, kan ikke huske dette for deg selv!). Ideen ville være enkelt, du har å bruke 100kN av last i trinn 1, og deretter fjerne 50kN av belastning i trinn 2, og fjern 50kN i trinn 3. Det er ingen måte å inkludere «platå» av last etter trinn 2 i analysen, og det vil bli utelatt., Logikken er enkel: det er ingen endringer i belastning = ingenting endringer i statisk!

Last inn på statisk

Hvis problemet ville være svært ikke-lineære, belastningen ville være «økt». Det er sjelden å være i stand til å anvende «full belastning» i ikkelineær analyse på «en go»! Vanligvis, solver ville gjelde dvs. 1kN hver «tilvekst». Dette betyr at etter 100 trinn, en full last av trinn 1 vil være anvendt. Dette gjør det enklere for brukeren å konvergere et riktig svar.,

Som bruker, kan du komme til å definere hvordan store intervaller solver skal bruke. Det er også noen algorythms å endre legg incrementation under analyse. Ulike solvers ønsker du å sette dette i differnet måter. Vanligvis FEA pakker bruk legg multiplikatorer for dette. Dette betyr, at du kan si noe sånt som: «i hvert inkrement gjelde flere 0,01 av alle lasten».

Awesome… men la oss komme til dynamikk, skal vi?, I dynamisk analyse du kan få den lastfordeling som ovenfor med en slik belastning definisjon:

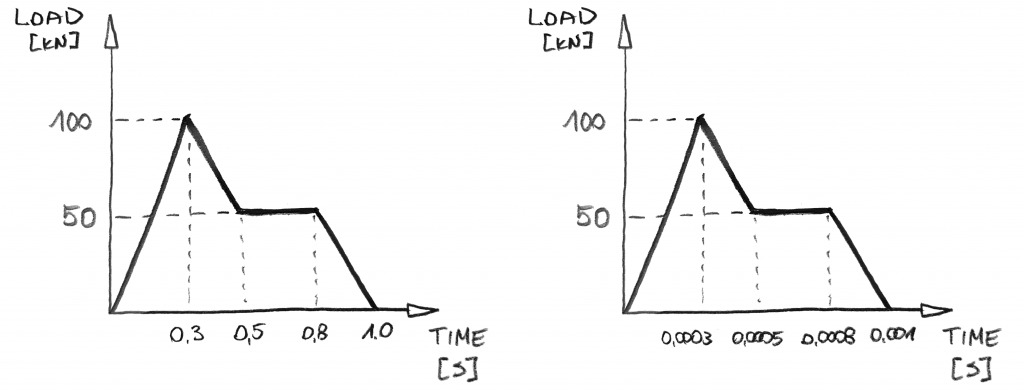
Umiddelbart, er det et par ting du kan merke:

• Det er ingen trinn! Dette er fordi i dynamisk analyse du vil ikke inkrement belastning. Du vil øke tiden! Og siden tiden går «hele tiden» fra null til den fastsatte verdien, kan du inkrement det i «one step».

• Tid er av essensen! Når det kommer til verdier av belastningen, over-kart er den samme., Men dette er ikke det samme dynamisk tilfelle! Figuren til høyre gjelder legg 1000x raskere! Dette er ikke noe du kan bare ignorere i dynamisk analyse!

generelt sett, når du ønsker å løse et dynamisk problem, du ber din solver til å gjøre én ting. Spør du den til å beregne serien av tid av gangen, for å se hva som skjer i modellen. I hver av disse trinn, tar litt lenger tid øker. Dette er selvfølgelig også endringer legg i modellen. Dette er grunnen til at du trenger å ha en tidsavhengig diagram for belastning., Så solver «vet» hva lasten skal brukes på en tid inkrement. Til denne grad, det fungerer på samme måte som legg incrementation i statisk analyse. Bonusen er, at siden du er stigende tid, treghet virkninger som kan tas i betraktning når ting skjer raskt nok.

Til denne grad, både implisitt og eksplisitt analyse gjør mer eller mindre det samme. De deler seg «analyser tid» i små trinn, og deretter analysere hva som skjer i din modell, ett trinn av gangen etter den andre. Men her er der likheter slutt!, Du ser, det er forskjellige tilnærminger til tid incrementation du kan ha!

Implisitt vs Eksplisitt – Når Tid som Virkelig betyr noe!

Du nettopp har lært, at for å beregne den ikke-lineære dynamiske problemet, må du trinnvis øke «analyse tid». Som jeg allerede har nevnt, kan dette gjøres på to måter.

jeg vil starte med en implisitt tilnærming. Jeg tror det er lettere å forstå siden det fungerer mer eller mindre det samme som legg incrementation i ikke-lineær statisk analyse!,

Hvordan Implisitt Analyse Fungerer:

Først av alt, implisitt synes å være en mer «grunnleggende» løsning. I hovedsak det fungerer akkurat som du ville tror det skal!

• for det Første, i hvert tidsintervallet «global likevekt» i modellen er etablert. Dette betyr at hvert steg har til å møtes (dette skjer i iterasjoner).

• Etter global likevekt er ok, solver beregner alle de lokale finite element variabler (påkjenninger osv. for dette inkrement.,

• Fordeler: Siden global likevekt er verifisert på hver tid intervaller, de trinn kan være STOR!
• Ulemper: Hver gang tilvekst regner sakte, siden iterasjoner er nødvendig for å få til global likevekt.

Hvis du er kjent med ikke-lineær statisk analyse vil du føle deg «hjemme» med en implisitt solver. Som bruker, kan du vanligvis får til å si hvor stor den tid intervaller du ønsker å ha. Dette er en stor fordel… det er lett å gå glipp av., Fordi Eksplisitt solver ikke tilbyr en slik mulighet!

La oss ta en titt på eksplisitt incrementation neste!

Hvordan Eksplisitt Analyse Fungerer:

Dette er funky. Det fungerer på en måte, at du ikke trenger å møtes hvert trinn! Det er ingen konvergens kriterier for å kontrollere og… ingen iterasjoner! I stedet for verifisere den «global likevekt» solver forutsetter at likevekt «bare eksisterer». Dette betyr at brukeren går rett inn i beregningen av lokale finite element variabler!, Som en slik fremgangsmåte har bare ett trinn:

• Beregne alle de lokale finite element variabler for gitt økning, og flytte til den neste!

• Fordeler: Hvert inkrement beregner ekstremt fort!
• Ulemper: For at dette skal fungere, er det tid for steg har til å være SVÆRT liten. Ellers, det er umulig å opprettholde denne balansen som er antatt å «bare eksisterer». For å oppnå dette, har brukeren ikke har direkte kontroll over hvor store økninger eksplisitt solver vil ta., Solver seg selv beregner hvor liten timesteps er fortsatt ok. Og de akseptabel tid intervaller er SUPER LITEN! Dette er grunnen til eksplisitt problemer bør vare i brøkdeler av sekund! Hvis de ville vare sekunder… ville du trenger millioner av trinn!

for Å raskt oppsummere det: både implisitt og eksplisitt solvers løse de samme tingene. Den eneste forskjellen er, hvordan de metoder tilvekst tid.

Teknisk, både skal produsere samme resultat for alle tilfeller., Tross alt, kan du analysere det samme problemet med begge metodene. Åpenbart, svaret kan ikke være avhengig av metoden som brukes til å løse problemet! Men selvfølgelig, du vil bare plukke en av de tilnærminger for din neste problemet, slik som en? La oss finne ut!

Hva er Bedre for Deg: Implisitt eller Eksplisitt?

Vi allerede er enige om at du kan bruke både implisitt og eksplisitt solvers å løse samme type problemer. Den eneste forskjellen er i tilnærming til tid incrementation. Men det er ikke en triviell ting!, Hvis forskjellen ville være liten, ingen ville vare å gjennomføre begge deler! Så la oss ta en titt på hvordan denne gangen incrementation innflytelse ting!

Både implisitt og eksplisitt solvers har noen områder der de skinner. Og det er en overlapping i deres bruk:

• implisitt analyse-lar deg velge hvor stor tidsintervallet bør være! Denne tilveksten vil ta litt tid å beregne siden det har til å gå for global likevekt første. Men du kan gjøre det «rimelig store» for analyse.,

• Eksplisitt tid intervaller beregne virkelig fort! Rett og slett fordi de ikke gjentas for global likevekt… men tidsintervallet det er ikke ditt valg! Solver bare antar, at «akseptabelt» tidsintervallet er «X» og går med det. Merk at denne «X» kan lett bli noe sånt som 5e-7s… Dette er super liten! For å løse et problem skjer over 1s, ville du trenger 2 000 000 trinn!

• Og det er det! Hastigheten på computing er akkurat forskjellen mellom implisitt og eksplisitt., Selvfølgelig, størrelsen av uttrykkelig trinn avhenger av modellen og computing ganger er avhengig av din maskinvare. Det er imidlertid enkle observasjoner som vi kan lett gjøre:

Bruk implisitt for «slow analyse»!

Hvis ting du beregne skjer over flere sekunder… det er ingen mening i å bruke eksplisitt solver. Det vil ta en evighet å grave seg gjennom millioner av tid intervaller som trengs for dette til å regne ut!, I stedet, satt en «rimelig» tid, trinn for implisitt analyse (la oss si 100 lik tid intervaller for analyse). Sikker, hver av dem implisitt tid intervaller vil beregne mye lenger enn en enkelt eksplisitt inkrement. Men ikke lenger enn hundrevis av tusenvis av dem!

Bruk eksplisitt for «rask analyse»!

Dette er opplagt, ikke sant? Hvis det du beregne skjer i liten brøkdel av et sekund eksplisitt er din venn., I en implisitt analyse, din tid tilvekst ville være super liten… kanskje til og med så liten som økningen i eksplisitt analyse. I et slikt tilfelle eksplisitt analyse vil kjøre MYE raskere siden det ikke krever «global likevekt» iterasjoner. Den implisitte analyse krever de iterasjoner (uavhengig av tid steg!).

Innimellom ting!

selvfølgelig, det er problemer som skjer i midten (som en innvirkning med 5m/s hastighet)., Vanligvis kan du løse et slikt problem med både solvers, men det kan være irriterende.

jeg håper at dette hjelper deg å velge riktig tilnærming til din dynamiske problemer. Selvfølgelig, i slutten, erfaring er den beste guiden! Hvis du er i tvil, kan du kjøre noen av dine typiske problemer, både implisitt og eksplisitt. Denne måten, vil du være i stand til å sammenligne resultatene (de bør være den samme). Men hva er mer viktig, vil du være i stand til å sammenligne computing ganger! Dette vil gi deg en mulighet til å sjekke, hva er en bedre tilnærming for deg!,

Hvordan eksplisitte antakelser gang trinn størrelse?

Vel, det er alt fint og dandy så langt, men jeg tror det ville være hyggelig å ta ett stort problem. Og det er… hvis du ikke velge tid skritt i din eksplisitt analyse… så hvem gjør det?

Den matematiske forklaringen ville kreve en diskusjon om maksimal naturlig frekvens. Dette er fordi maksimal «fremdeles er akseptabel,» tidsintervallet er omvendt proporsjonal med maksimal naturlig frekvens. Slike beregninger kan gjøres, selvfølgelig., Utfallet avhenger av mesh av modellen (hvor mange elementer som er der, osv.). Men vi vil ikke gå der, og det er 2 grunner: for det første, jeg liker ikke matematikk (!). For det andre, dette er ikke hvordan solvers gjøre det til slutt, selv om dette er den «riktige måten».

brukeren kan beregne maksimal naturlig frekvens, selvfølgelig, men dette tar litt tid. Og siden det må gjøres i hvert eksplisitt tidsintervallet (det kan være nok av dem!)… yikes!, Heldigvis, det er en måte å pent beregne denne verdien, ved å analysere hver finite element i systemet separat! Den fysiske tolkningen av denne estimering (vanligvis brukes i solvers) er:

kvalitetstid økning i eksplisitt analyse:

tidsintervallet eksplisitt analyse er svært kort. Det er den tiden der en elastisk wave (dvs. innvirkning wave) kan reise gjennom et enkelt finite element i modellen. Selvfølgelig, dette er verifisert for alle begrensede elementer i modellen, og den minste tid som er valgt.,

Som du kan se, det er 2 komponenter til de eksplisitte tid komponent:

• Elastisk bølge hastighet (aka speed of sound i materialet)! Dette avhenger bare på det materialet du har i modellen (og det er forskjellig for ulike materialer selvfølgelig!). Du trenger Unge Elastisitetsmodul E, stofftetthet og Poisson-Rasjon (i 2D-og 3D-problemer). Det er lett å finne tabeller som liste elastisk bølge hastigheter i ulike materialer. Bare for referanse i stål, dette er rundt 5200m/s (mange metaller er rundt 4500-5500m/s).,

• – Element størrelse (og kvalitet)! Du har bølge hastighet, men det er ikke nok! Å vite den tid det er behov for å reise gjennom elementet du trenger å vite elementet «lengde». Mens denne er super enkel i 1D elementer (de rett og slett har lengde) det blir vanskelig i 2D og 3D. Denne lengden er ikke «bare» den korteste av elementet kantene siden elementer kan ha ganske dårlig geometri. Det er ting solver gjør for å beregne dette. I 2D-det kan være et element området dividert med den maksimale kanten lengde., I 3D-det kan bety at volumet av element er dividert med den maksimale side-området. Dette er grunnen til at ikke bare element størrelse, men også elementer kvaliteten er så viktig i eksplisitt analyse! Tross alt… alt du trenger er en dårlig element for å virkelig skade din computing tid!

jeg har lest et eller annet sted, at mens det ovenfor er «presis» løsning, solvers bruker ofte «sikkerhetsfaktorer» på dette. Hvis du får en høyere tid tilvekst enn elastisk bølge «fartsgrense» matematisk feil oppstår. Siden beregningene er brukt, solvers ofte redusere tiden trinn «bare i tilfelle»., Vanligvis, reduksjonsfaktor er rundt 0.9, men dette kan variere fra solver til å solver selvfølgelig.

Masse skalering!

I slutten, vil jeg nevne noe raskt.

Du har mest sannsynlig lagt merke til, at tiden trinn i eksplisitte bare avhenger mesh, Unge Modulus, og tetthet. Å redusere Unge Modulus kan ikke være ideelt for kurset, og du trenger ofte et lite inngrep til å analysere informasjon. Men i «lav dynamisk» problemer kan du prøve å øke eksplisitt gang trinn ved å øke stofftetthet.,

Denne er kalt «mass scaling». FEA-pakker selv tilbyr løsninger der tettheten er økte bare i de elementene som «bestemmer» om tidsintervallet. Dette betyr at noen ganger er det bare små deler av modellen får tyngre! I noen analyser, du kan «slippe unna» med økende massen av modellen. Hvis det er tilfelle, kan dette være en løsning for deg. Bare vær oppmerksom på, at dette ikke endre hvordan modellen fungerer! Når høy akselerasjoner er involvert, er det best å være forsiktig!

Oppsummering

Fin!, Du har her, takk for at du leser! La oss bryte dette opp, så det er lettere å huske!

• Dynamisk analyse innebærer tid! Når du bruker laster, de må være definert i en tid funksjon. Ofte er dette et lineært forhold. Men dette endrer ikke at tiden som belastning påføres spiller en betydelig rolle (spesielt hvis denne tiden er kort!).

• 2 smaker av dynamisk analyse! Du kan løse den «virkelige» dynamiske problemer med implisitte og eksplisitte algoritmer. Begge er fine, og ikke en eneste en av dem er «bedre»., Men jeg må si at den eksplisitte solver er en del av færre FEA-pakker. Siden ikke alle FEA pakken selv har en, den eksplisitte solver er sett på som en «mer avansert» ting.

• implisitt solver er veldig bra hvis ting i din analyse skje relativt langsomt. La oss si at analysen er lengre enn 1s uten noen brå ting skjer i løpet av den tiden. Fordelen er at du kan velge hvor stor tidsintervallet du vil. Selv om enkelt tilvekst tar lengre tid å beregne, det er mye færre av dem!,

• eksplisitt solver er flott for rask skjer ting (la oss si raskere enn 0,1 s). Du får ikke til å velge tidsintervallet her – solver vil automatisk sette det. Mens de er vanligvis super liten, i hvert fall de beregne mye raskere enn den «implisitte seg». Eksplisitt solver beregner hvor stor tidsintervallet bør være. Dette avhenger av lydens hastighet i materialet ditt, minimal finite element størrelse (og element kvalitet!). I noen tilfeller kan du endre tetthet (selv automatisk bare i «avgjøre elementer»!) for å justere dette tidsintervallet., Dette fungerer, fordi lydens hastighet i materialet avhengig av tetthet! Dette kalles «mass scaling».