Good Mood

Visa mobil meddelande Visa alla anteckningar Dölj alla anteckningar

avsnitt 4-6 : formen på en graf, del II

i föregående avsnitt såg vi hur vi kunde använda det första derivatet av en funktion för att få lite information om grafen för en funktion. I det här avsnittet kommer vi att titta på den information som det andra derivatet av en funktion kan ge oss en om grafen för en funktion.

innan vi gör detta behöver vi ett par definitioner ur vägen. Huvudkonceptet som vi ska diskutera i det här avsnittet är konkavitet. Konkavitet är lättast att se med en graf(vi ger den matematiska definitionen i lite).,

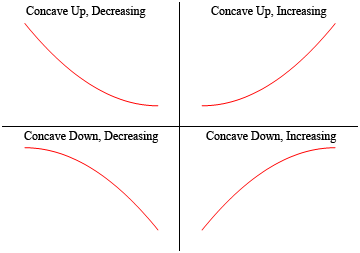
så, en funktion är konkav upp om det ”öppnar” upp och funktionen är konkav ner om det ”öppnar” ner. Observera också att konkavitet inte har något att göra med att öka eller minska. En funktion kan konkav upp och antingen öka eller minska. På samma sätt kan en funktion vara konkav ner och antingen öka eller minska.

det är förmodligen inte det bästa sättet att definiera konkavitet genom att säga vilket sätt det ”öppnar” eftersom det här är en något nebulös definition. Här är den matematiska definitionen av konkavitet.,

Definition 1

för att visa att graferna ovan faktiskt har concavity hävdat ovan här är grafen igen (blåst upp lite för att göra saker tydligare).

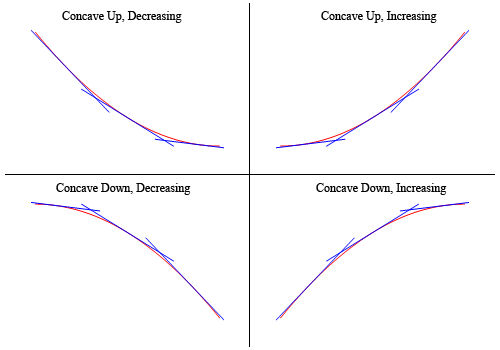
så, som du kan se, i de två övre graferna är alla tangentlinjer skisserade i alla under grafen för funktionen och dessa är konkava upp. I de nedre två graferna ligger alla tangentlinjerna ovanför grafen för funktionen och dessa är konkava ner.,

Observera igen att konkavitet och den ökande/minskande aspekten av funktionen är helt separat och inte har något att göra med varandra. Detta är viktigt att notera eftersom eleverna ofta blandar dessa två upp och använder information om en för att få information om den andra.

det finns ytterligare en definition som vi behöver för att komma ur vägen.

Definition 2

nu när vi har alla konkavitetsdefinitioner ur det sätt vi behöver för att få det andra derivatet i blandningen. Vi började trots allt med det här avsnittet och sa att vi skulle använda det andra derivatet för att få information om grafen. Följande faktum avser det andra derivatet av en funktion till dess konkavitet. Beviset på detta faktum finns i bevisen från Derivattillämpningsavsnittet i extrakapitlet.

faktum

Så, vad detta faktum säger oss är att inflektionspunkterna kommer att vara alla punkter var det andra derivatändringstecknet., Vi såg i föregående kapitel att en funktion kan ändra tecken om det är antingen noll eller inte existerar. Observera att vi arbetade med det första derivatet i föregående avsnitt men det faktum att en funktion som eventuellt ändrar tecken där det är noll eller inte existerar har ingenting att göra med det första derivatet. Det är helt enkelt ett faktum som gäller för alla funktioner oavsett om de är derivat eller inte.,

detta berättar i sin tur att en lista över möjliga inflektionspunkter kommer att vara de punkter där det andra derivatet är noll eller inte existerar, eftersom det här är de enda punkterna där det andra derivatet kan ändra tecken.

var försiktig med att inte anta att bara för att det andra derivatet är noll eller inte existerar att punkten kommer att vara en böjningspunkt. Vi kommer bara att veta att det är en böjningspunkt när vi bestämmer konkaviteten på båda sidor av den. Det kommer bara att vara en böjningspunkt om konkaviteten är annorlunda på båda sidor av punkten.,

nu när vi vet om konkavitet kan vi använda denna information samt den ökande / minskande informationen från föregående avsnitt för att få en ganska bra uppfattning om hur en graf ska se ut. Låt oss ta en titt på ett exempel på det.

Vi kan använda föregående exempel för att illustrera ett annat sätt att klassificera några av de kritiska punkterna i en funktion som relativa maximum eller relativa minimumvärden.

som vi ser i lite måste vi vara mycket försiktiga med \(x = 0\)., I det här fallet är det andra derivatet noll, men det betyder faktiskt inte att \(x= 0\) inte är ett relativt minimum eller maximalt. Vi kommer att se några exempel på detta om lite, men vi måste få lite annan information om först.

det är också viktigt att notera här att alla kritiska punkter i detta exempel var kritiska punkter där det första derivatet var noll och detta krävs för att detta ska fungera. Vi kommer inte att kunna använda detta test på kritiska punkter där derivatet inte existerar.,

här är testet som kan användas för att klassificera några av de kritiska punkterna i en funktion. Beviset på detta test finns i avsnittet bevis på Derivattillämpningar i kapitlet extramaterial.

andra Derivattest

den tredje delen av det andra derivattestet är viktigt att notera. Om det andra derivatet är noll kan den kritiska punkten vara någonting. Nedan är graferna med tre funktioner som alla har en kritisk punkt vid \(x = 0\), det andra derivatet av alla funktioner är noll vid \(x = 0\) och ändå uppvisas alla tre möjligheterna.,

den första är grafen av \(f\left( x \right) = {x^4}\). Denna graf har ett relativt minimum vid \(x = 0\).

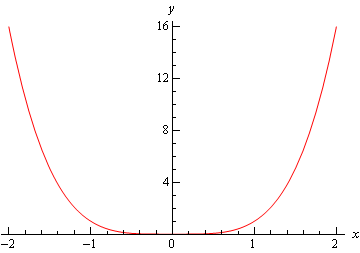
nästa är grafen för \(f\left( x \right) = – {x^4}\) som har ett relativt maximum vid \(x = 0\).

slutligen finns grafen \(f \ left (x \ right) = {x^3}\) och grafen hade varken ett relativt minimum eller ett relativt maximum vid \(x = 0\).

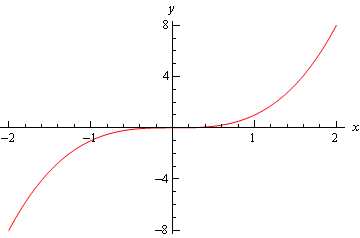
Så vi kan se att vi måste vara försiktiga om vi hamnar i det tredje fallet., För de tider då vi faller i detta fall måste vi tillgripa andra metoder för att klassificera den kritiska punkten. Detta görs vanligtvis med det första derivatestet.

låt oss gå tillbaka och ta en titt på de kritiska punkterna från det första exemplet och använd det andra Derivatestet på dem, om möjligt.

låt oss arbeta ytterligare ett exempel.