Good Mood

Bild här: Du gör en presentation av din Ph. D. avhandling om stabilitet vid ett av seminarierna. Allt går smidigt, och slutligen är det frågestund! Och någon ur det blå frågar: ”Vad är skillnaden mellan implicit och explicit tillvägagångssätt?”! Och eftersom du gör statisk stabilitet … du aldrig ens hört dessa villkor! Ja … har varit där gjort det!, Nu är jag lite klokare, så låt oss ta en närmare titt på skillnaderna mellan Implicit och Explicit analys

Implicit och Explicit analys skiljer sig åt i tillvägagångssättet till tidsökning. I Implicit analys varje gång ökningen måste konvergera, men du kan ställa in ganska lång tid steg. Explicit å andra sidan behöver inte konvergera varje ökning, men för att lösningen ska vara exakta tidsökningar måste vara super små.

det här låter ganska enkelt, eller hur?, Om du inte börjar tänka på saker som” vilken ska jag använda ”eller” hur liten ska den uttryckliga tidshöjningen vara ” och saker som det. Inga problem,jag har dig täckt!

låt oss dyka in!

dynamik som bäst – Implicit / Explicit!

du kommer att använda implicita och explicita lösare för att lösa dynamiska problem. Det betyder att du inte behöver veta det här om du gör statisk analys., Om du är osäker på skillnaden mellan statisk och dynamisk analys, läs det här inlägget först-det kommer att göra det lättare att förstå!

dynamisk analys i ett nötskal:

dynamisk analys löser problem med tröghetseffekter. De visas, när saker förändras snabbt i din modell (snabbt applicerade laster, effekter etc.). Ingenjörer brukar reffer till detta som”olinjär dynamisk”.

det bör noteras, som ofta ingenjörer kallar annan analys ”dynamisk” också., Saker som Modal analys eller forcerad Responsanalys som hanterar vibrationer. Ibland kallas de ”linjär dynamik”, men det är vanligtvis en bra idé att se till vad någon betyder när de använder en sådan fras. Medan ”linjära dynamiska” problem är riktigt intressanta, kommer jag inte att diskutera dem här. Du kan lära dig mer om dem läsa det här inlägget!

det första jag verkligen känner att jag måste betona är att implicita och explicita lösare löser samma problem!, Tänk på det inte som” olika lösare ” utan snarare som två olika sätt att lösa samma problem.

i många fall kan du använda både implicit och explicit lösare, och de kommer att producera samma resultat. Och jag tror att det är här vi måste börja!

hur dynamisk analys fungerar?

båda analyserna löser ett problem där sakernas hastighet är viktig. Detta innebär oftast att belastningen appliceras mycket snabbt. I sådana fall kommer du alltid att ”iterera” din last i tid., I grund och botten kommer du att använda tiden för att berätta lösaren ”vad som händer” och hur belastningen förändras.

För det första måste du definiera hur belastningen förändras i tid. Du brukar göra detta med hjälp av diagram, som den nedan:

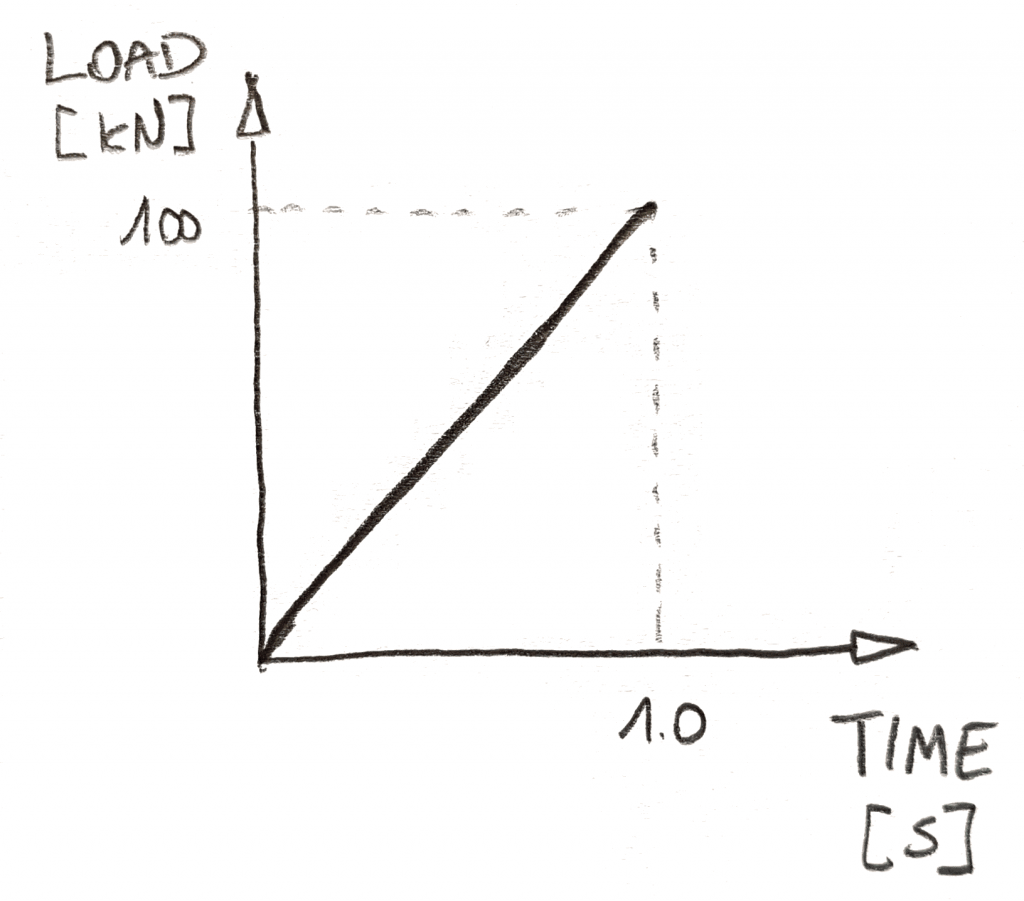
I icke-linjär dynamisk analys har tiden 2 Roller. För det första kan du berätta för lösaren när hur mycket belastning ska appliceras. Du måste helt enkelt implementera varje belastning med ett tidsberoende diagram. För det andra… tiden är inne! Det berättar lösaren hur snabbt Det går!,

Föreställ dig att du vill ha en sådan belastningssekvens:

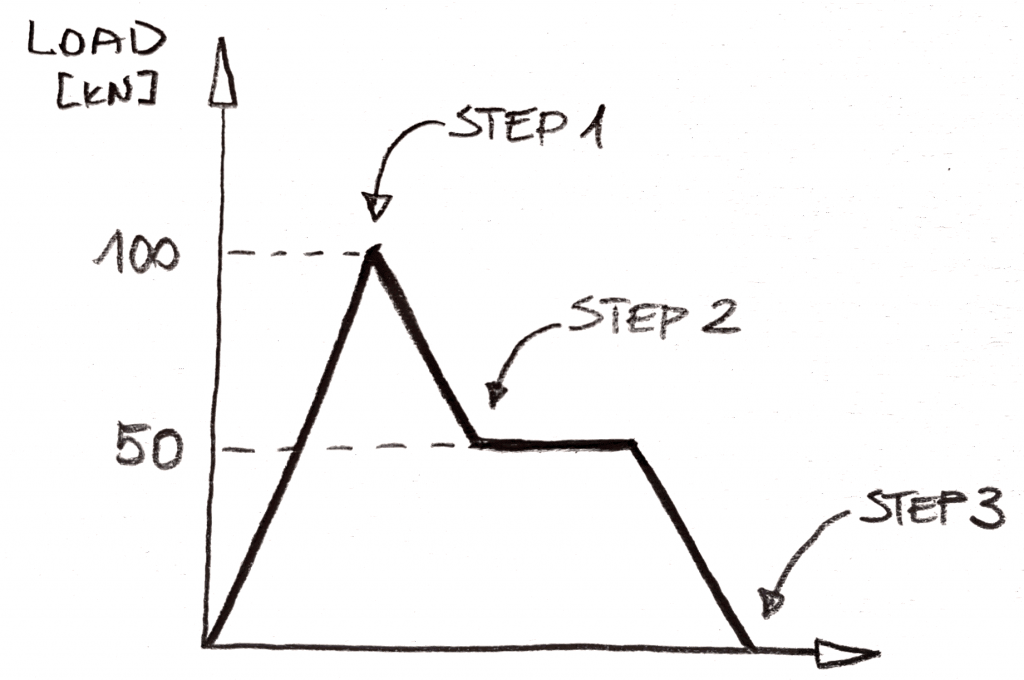
I statisk skulle detta vara en 3 ”steg” – analys (de kallas subcaser i NX Nastran, men jag tror att Abaqus faktiskt använde ”step” som ett namn, kan inte återkalla detta säkert men!). Tanken skulle vara enkel, du måste applicera 100kn av lasten i steg 1, Ta sedan bort 50kN av lasten i steg 2 och ta bort 50kN i steg 3. Det finns inget sätt att inkludera ”platån” av belastning efter steg 2 i analysen, och det kommer att utelämnas., Logiken är enkel: inga förändringar i belastning = ingenting förändras i statisk!

Belastningsstegringar i statiska

om problemet skulle vara mycket olinjärt skulle belastningen ”ökas”. Det är sällsynt att kunna applicera ”full belastning” i olinjär analys vid ”one go”! Vanligtvis skulle lösare gälla dvs 1KN varje ”ökning”. Detta innebär att efter 100 steg, en full belastning av steg 1 skulle tillämpas. Detta gör det lättare för lösare att konvergera ett korrekt svar.,

som användare får du definiera hur stora steglösare ska använda. Det finns också vissa algorythms att ändra Last incrementation under analys. Olika lösare vill att du ställer in detta på olika sätt. Vanligtvis använder FEA-paket lastmultiplikatorer för detta. Det betyder att du kan säga något som: ”i varje steg gäller ytterligare 0,01 av all belastning”.

häftigt… men låt oss komma till dynamik, ska vi?, I dynamisk analys kan du få lastfördelningen som ovan med en sådan belastningsdefinition:

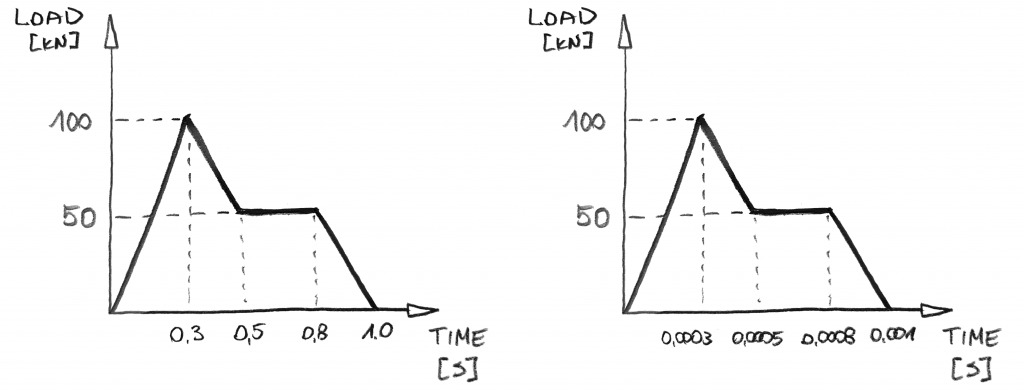
omedelbart finns det några saker du kan märka:

• det finns inga steg! Detta beror på att i dynamisk analys kommer du inte öka belastningen. Du kommer att öka tiden! Och eftersom tiden går ”ständigt” från noll till det föreskrivna värdet kan du öka det i ”ett steg”.

• tiden är kärnan! När det gäller värdena för lasten är ovanstående diagram desamma., Men det här är inte samma dynamiska fall! Diagrammet till höger gäller lasten 1000x snabbare! Detta är inte något du bara kan ignorera i dynamisk analys!

I allmänhet, när du vill lösa ett dynamiskt problem, ber du din lösare att göra en sak. Du ber den att beräkna serien av tidssteg, för att se vad som händer i modellen. I var och en av dessa steg ökar tiden något. Detta ändrar naturligtvis också belastningen i modellen. Det är därför du behöver ha ETT tidsberoende diagram för belastning., Så lösaren ” vet ” vilken belastning som ska appliceras vid vilken tidpunkt ökning. I denna utsträckning fungerar det samma som belastningsökning i statisk analys. Bonusen är, att eftersom du är incrementing tid, tröghet effekter kan beaktas när saker händer tillräckligt snabbt.

I denna utsträckning gör både implicit och explicit analys mer eller mindre samma sak. De delar upp ”analystiden” i små steg och analyserar sedan vad som händer i din modell en ökning av tiden efter den andra. Men här är där likheterna slutar!, Du ser, det finns olika sätt att öka tiden du kan ha!

Implicit vs Explicit – när tiden verkligen betyder något!

du lärde dig bara att för att beräkna det icke-linjära dynamiska problemet måste du stegvis öka ”analystid”. Som jag redan nämnde kan detta göras på två sätt.

Jag börjar med det implicita tillvägagångssättet. Jag tror att det är lättare att förstå eftersom det fungerar mer eller mindre samma som belastningsökning i olinjär statisk analys!,

hur Implicit analys fungerar:

först och främst verkar implicit vara en mer ”grundläggande” lösning. I huvudsak fungerar det precis som du skulle tro att det borde!

• för det första upprättas ”global equilibrium” i modellen i varje steg. Detta innebär att varje ökning måste konvergera (detta händer i iterationer).

• efter att global equilibrium är ok beräknar solver alla lokala ändliga elementvariabler (påfrestningar etc. för denna ökning.,

• fördelar: eftersom global jämvikt verifieras vid varje steg kan dessa steg vara stora!
• nackdelar: varje gång inkrement beräknas långsamt, eftersom iterationer behövs för att komma till den globala jämvikten.

om du är bekant med den icke-linjära statiska analysen kommer du att känna ”hemma” med den implicita lösaren. Som användare får du vanligtvis säga hur stora tidsstegren du vill ha. Detta är en stor fördel … som är lätt att missa., Eftersom Explicit lösare inte erbjuder en sådan möjlighet!

Låt oss ta en titt på explicit incrementation nästa!

hur Explicit analys fungerar:

den här är funky. Det fungerar på ett sätt, att du inte behöver konvergera varje steg! Det finns inga konvergenskriterier att kontrollera och … inga iterationer! I stället för att verifiera den” globala jämviktslösaren ”förutsätter att jämvikten ” helt enkelt existerar”. Detta innebär att lösaren går rakt in i beräkningen av lokala ändliga elementvariabler!, Som sådan procedur har bara ett steg:

• beräkna alla lokala ändliga elementvariabler för given ökning och flytta till nästa!

• fördelar: varje ökning beräknar extremt snabbt!
• nackdelar: för att detta ska fungera måste tidssteget vara extremt litet. Annars är det omöjligt att upprätthålla denna jämvikt som antas ”helt enkelt existera”. För att uppnå detta, användaren har inte direkt kontroll över hur big – time steg explicit lösare kommer att ta., Solver själv beräknar hur små timesteps fortfarande är ok. Och de acceptabla tidshöjningarna är SUPER små! Det är därför explicita problem borde vara fraktioner av den andra! Om de skulle sista sekunderna … skulle du behöva miljontals steg!

för att snabbt sammanfatta det: både implicita och explicita lösare löser samma saker. Den enda skillnaden är, hur dessa metoder ökar tiden.

tekniskt sett bör båda ge samma resultat för alla fall., När allt kommer omkring kan du analysera samma problem med båda tillvägagångssätten. Självklart kan svaret inte bero på vilken metod som används för att lösa problemet! Men självklart väljer du bara ett av tillvägagångssätten för ditt nästa problem,så vilken? Låt oss ta reda på det!

Vad är Bättre för Dig: Implicit eller Explicit?

vi har redan kommit överens om att du kan använda både implicita och explicita lösare för att lösa samma typ av problem. Den enda skillnaden är i inställning till tidsökning. Men det är inte en trivial sak!, Om skillnaden skulle vara liten, skulle ingen bry sig om att genomföra båda! Så låt oss ta en titt på hur denna gång incrementation påverkar saker!

både implicita och explicita lösare har några områden där de lyser. Och det finns en överlappning i deras användning:

• den implicita analysen låter dig välja hur stor tidsstegringen ska vara! Denna ökning kommer att ta lite tid att beräkna eftersom den måste iterera för global jämvikt först. Men du kan göra det ”ganska stort” för din analys.,

• Explicit tidssteg beräkna riktigt snabbt! Helt enkelt för att de inte itererar för global jämvikt… men tiden ökar det finns inte ditt val! Solver förutsätter helt enkelt att” acceptabel ”tidsökning är” X ” och går med den. Observera att denna ” X ” lätt kan vara något som 5e-7s … detta är super liten! För att lösa ett problem som händer över 1s, skulle du behöva 2 000 000 steg!

• Och det är det! Datorhastigheten är exakt skillnaden mellan implicit och explicit., Naturligtvis beror storleken på explicit steg på din modell och datortider på din hårdvara. Det finns dock enkla observationer som vi enkelt kan göra:

använd implicit för”långsam analys”!

om det du beräknar händer under flera sekunder… är det ingen mening att använda explicit lösare. Det kommer att ta för evigt att gräva igenom de miljontals tidssteg som behövs för att detta ska beräknas!, Ställ istället in ett ”rimligt” tidssteg för implicit analys (låt oss säga 100 lika tidssteg för din analys). Visst, var och en av dessa implicita tidssteg kommer att beräkna mycket längre än en enda explicit ökning. Men inte längre än hundratusentals av dem!

använd explicit för”snabb analys”!

detta är uppenbart, eller hur? Om det du beräknar händer i den lilla fraktionen av en andra explicit är din vän., I en implicit analys skulle din tidsökning vara super liten … kanske lika liten som ökningen i explicit analys. I ett sådant fall kommer explicit analys att köras mycket snabbare eftersom det inte kräver ”global jämvikt” iterationer. Den implicita analysen kräver dessa iterationer (oavsett tidssteg!).

Mellan saker!

naturligtvis finns det problem som händer i mitten (som en inverkan med 5m/s hastighet)., Vanligtvis kan du lösa ett sådant problem med båda lösarna, men det kan vara irriterande.

jag hoppas att detta hjälper dig att välja en lämplig inställning till dina dynamiska problem. Naturligtvis är upplevelsen i slutändan den bästa guiden! Om du är osäker, kör några av dina typiska problem i både implicit och explicit. På så sätt kommer du att kunna jämföra resultat (de borde vara desamma). Men vad som är viktigare, kommer du att kunna jämföra datortider! Detta ger Dig möjlighet att kontrollera, vad är ett bättre tillvägagångssätt för dig!,

hur explicit gissningar tid steg storlek?

Tja, det är allt trevligt och dandy hittills, men jag tror att det skulle vara trevligt att ta itu med en stor fråga. Och det är… om du inte väljer tidssteget i din explicita analys… vem gör det då?

den matematiska förklaringen skulle kräva en diskussion om den maximala naturliga frekvensen. Detta beror på att maximal” fortfarande acceptabel ” tidsökning är omvänt proportionell mot den maximala naturliga frekvensen. Sådana beräkningar kan naturligtvis göras., Resultaten beror på modellens nät (hur många element finns det etc.). Men vi kommer inte att åka dit, och det finns 2 anledningar till varför: för det första gillar jag inte matematik (!). För det andra är det inte så här lösare gör det i slutändan, även om det här är ”rätt sätt”.

solvaren kan naturligtvis beräkna den maximala naturliga frekvensen, men det tar ganska lång tid. Och eftersom det skulle behöva göras i varje explicit tidsökning (det kan finnas gott om dem!- usch!, Lyckligtvis finns det ett sätt att fint uppskatta detta värde genom att analysera varje ändligt element i systemet separat! Den fysiska tolkningen av denna uppskattning (som vanligen används i lösare) är:

Maximal tidsökning i explicit analys:

tidsökning i explicit analys är mycket kort. Det är den tid då en elastisk våg (dvs slagvåg) kan resa genom ett enda ändligt element i din modell. Naturligtvis är detta verifierat för alla ändliga element i din modell, och den minsta tiden är vald.,

som du kan se finns det 2 komponenter till den explicita tidskomponenten:

• elastisk våghastighet (aka ljudets hastighet i ditt material)! Detta beror bara på det material du har i din modell(och det är annorlunda för olika material förstås!). Du behöver den unga modul E, materialtäthet och Poisson Ration (i 2D och 3D-problem). Det är lätt att hitta tabeller som listar elastiska våghastigheter i olika material. Bara för referens i stål, Detta är runt 5200m/s (många metaller är runt 4500-5500m / s).,

• Elementstorlek (och kvalitet)! Du har våghastigheten, men det räcker inte! För att veta den tid det behöver resa genom elementet behöver du veta elementet ”längd”. Även om detta är super enkelt i 1D-element (de har helt enkelt längd) blir det knepigt i 2D och 3D. Denna längd är inte ”helt enkelt” den kortaste av elementkanterna eftersom element kan ha ganska dålig geometri. Det finns saker som solver gör för att beräkna detta. I 2D kan det vara ett elementområde dividerat med maximal kantlängd., I 3D kan det innebära att elementets volym divideras med det maximala sidoområdet. Det är därför inte bara elementstorlek utan även element kvalitet är så viktigt i explicit analys! När allt kommer omkring… allt du behöver är ett dåligt element för att verkligen skada din datortid!

jag har läst någonstans, att medan ovanstående är den ”exakta” lösningen använder lösare ofta ”säkerhetsfaktorer” på detta. Om du får en högre tidsökning än den elastiska vågen ”hastighetsgräns” uppstår matematiska fel. Eftersom uppskattningar används, minskar lösare ofta tidssteget ”just in case”., Vanligtvis är reduktionsfaktorn cirka 0,9, men detta kan variera från lösare till lösare förstås.

massskalning!

I slutändan vill jag nämna något snabbt.

du märkte troligtvis att tidssteget i explicit bara beror på nät, ung modul och densitet. Att minska ung modul kanske inte är idealisk, och du behöver ofta ett litet nät för att analysera detaljer. Men i” låga dynamiska ” problem kan du försöka öka den explicita tiden steg genom att öka materialtätheten.,

detta kallas ”massskalning”. FEA-paket erbjuder även lösningar där tätheten endast ökas i de element som” bestämmer ” om tidsökning. Det betyder att ibland blir bara små delar av din modell tyngre! I viss analys kan du ”komma undan” med att öka massan av din modell. Om så är fallet kan detta vara en lösning för dig. Bara vara medveten om, att detta ändrar hur din modell beter sig! När höga accelerationer är inblandade, är det bäst att vara försiktig!

sammanfattning

trevligt!, Du kom hit, tack för att du läste! Låt oss avsluta det här, så det är lättare att komma ihåg!

• dynamisk analys innebär tid! När du använder laster måste de definieras i en tidsfunktion. Ofta är detta ett linjärt förhållande. Men det här ändras inte, att den tid då belastningen appliceras spelar en viktig roll (speciellt om den här tiden är kort!).

• 2 smaker av dynamisk analys! Du kan lösa de” riktiga ” dynamiska problemen med implicita och explicita algoritmer. Båda är bra, och inte en enda av dem är ”bättre”., Men jag borde säga att den explicita lösaren är en del av färre FEA-paket. Eftersom inte varje FEA-paket ens har en, ses den explicita lösaren som en” mer avancerad ” sak.

• den implicita lösaren är riktigt bra om saker i din analys händer relativt långsamt. Låt oss säga att analysen är längre än 1s utan några abrupta saker som händer under den tiden. Fördelen är att du kan välja hur stor tid inkrement du vill. Även om den enda ökningen tar längre tid att beräkna, finns det mycket färre av dem!,

• den explicita lösare är bra för snabba händer saker (låt oss säga snabbare än 0,1 s). Du får inte välja tidsökning här – solver ställer in den automatiskt. Medan de vanligtvis är super små, beräknar de åtminstone mycket snabbare än de”implicita”. Explicit solver beräknar hur stor tidsökning ska vara. Detta beror på ljudhastigheten i ditt material, minimal ändlig elementstorlek (och elementkvalitet!). I vissa fall kan du ändra densitet (även automatiskt endast i ”avgörande element”!) för att justera denna tidsökning., Detta fungerar, eftersom ljudets hastighet i ditt material beror på dess densitet! Detta kallas ”massskalning”.