Good Mood

Afficher L’avis Mobile afficher toutes les Notes masquer toutes les Notes

Section 4-6 : La Forme d’un Graphique, la Partie II

Dans la section précédente, nous avons vu comment nous pourrions utiliser la dérivée première d’une fonction permettant d’obtenir quelques informations sur le graphique d’une fonction. Dans cette section, nous allons regarder les informations que la dérivée seconde d’une fonction peut nous donner un sujet de la représentation graphique d’une fonction.

avant de faire cela, nous aurons besoin de quelques définitions. Le concept principal dont nous parlerons dans cette section est la concavité. La concavité est plus facile à voir avec un graphique (nous donnerons la définition mathématique dans un peu).,

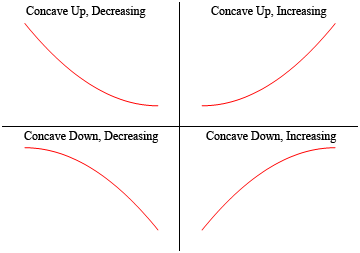
Donc, une fonction est concave si il « s’ouvre” et la fonction est concave vers le bas si il « s’ouvre” vers le bas. Notez également que la concavité n’a rien à voir avec l’augmentation ou la diminution. Une fonction peut être concave vers le haut et soit croissante ou décroissante. De même, une fonction peut être concave vers le bas et soit croissante ou décroissante.

ce n’est probablement pas la meilleure façon de définir la concavité en disant de quelle façon elle « ouvre” car c’est une définition quelque peu nébuleuse. Voici la définition mathématique de la concavité.,

définition 1

pour montrer que les graphiques ci-dessus ont en fait une concavité revendiquée ci-dessus, voici le graphique à nouveau (soufflé un peu pour rendre les choses plus claires).

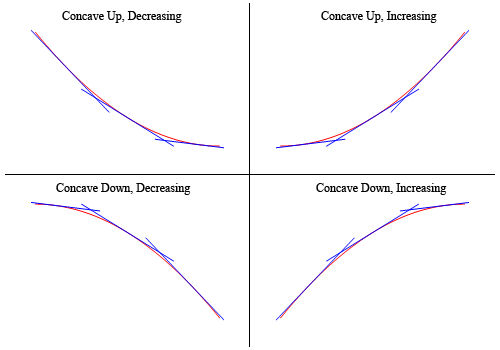
ainsi, comme vous pouvez le voir, dans les deux graphiques supérieurs, toutes les lignes tangentes esquissées sont toutes sous le graphique de la fonction et celles-ci sont concaves vers le haut. Dans les deux graphiques inférieurs, toutes les lignes tangentes sont au-dessus du graphique de la fonction et celles-ci sont concaves vers le bas.,

encore une fois, notez que la concavité et l’aspect croissant / décroissant de la fonction sont complètement séparés et n’ont rien à voir l’un avec l’autre. Ceci est important à noter parce que les étudiants mélangent souvent ces deux et utilisent des informations sur l’un pour obtenir des informations sur l’autre.

Il y a une définition de plus que nous devons sortir de la route.

Définition 2

maintenant que nous avons toutes les définitions de concavité de la manière dont nous devons apporter la dérivée seconde dans le mélange. Après tout, nous avons commencé cette section en disant que nous allions utiliser la dérivée seconde pour obtenir des informations sur le graphique. Le fait suivant relie la dérivée seconde d’une fonction à sa concavité. La preuve de ce fait se trouve dans la section preuves D’Applications dérivées du chapitre Extras.

fait

donc, ce que ce fait nous dit, c’est que les points d’inflexion seront tous les points où la dérivée seconde change le signe., Nous avons vu dans le chapitre précédent qu’une fonction peut changer de signe si elle est nulle ou n’existe pas. Notez que nous travaillions avec la dérivée première dans la section précédente mais le fait qu’une fonction change éventuellement de signe où elle est nulle ou n’existe pas n’a rien à voir avec la dérivée première. C’est simplement un fait qui s’applique à toutes les fonctions, qu’elles soient dérivées ou non.,

ceci nous indique à son tour qu’une liste de points d’inflexion possibles sera les points où la dérivée seconde est nulle ou n’existe pas, car ce sont les seuls points où la dérivée seconde peut changer de signe.

attention toutefois à ne pas faire l’hypothèse que juste parce que la dérivée seconde est nulle ou n’existe pas que le point sera un point d’inflexion. Nous saurons seulement que c’est un point d’inflexion une fois que nous déterminerons la concavité des deux côtés de celui-ci. Ce ne sera un point d’inflexion que si la concavité est différente des deux côtés du point.,

maintenant que nous connaissons la concavité, nous pouvons utiliser ces informations ainsi que les informations croissantes / décroissantes de la section précédente pour avoir une assez bonne idée de ce à quoi devrait ressembler un graphique. Prenons un oeil à un exemple.

Nous pouvons utiliser l’exemple précédent pour illustrer une autre façon de classer certains des points critiques d’une fonction en tant que maximums relatifs ou minimums relatifs.

Comme nous le verrons dans un peu, nous devrons être très prudents avec \(x = 0\)., Dans ce cas, la dérivée seconde est nulle, mais cela ne signifie pas que \(x = 0\) n’est pas un minimum ou un maximum relatif. Nous verrons quelques exemples de cela dans un peu, mais nous devons d’abord prendre en charge d’autres informations.

Il est également important de noter ici que tous les points critiques dans cet exemple étaient des points critiques dans lesquels la dérivée première était nulle et ceci est nécessaire pour que cela fonctionne. Nous ne pourrons pas utiliser ce test sur des points critiques où la dérivée n’existe pas.,

Voici le test qui peut être utilisé pour classer certains des points critiques d’une fonction. La preuve de ce test se trouve dans la section preuves d’Applications dérivées du chapitre Extras.

test de la dérivée seconde

la troisième partie du test de la dérivée seconde est importante à remarquer. Si la dérivée seconde est nulle alors le point critique peut être n’importe quoi. Voici les graphiques de trois fonctions qui ont toutes un point critique à \(x = 0\), la dérivée seconde de toutes les fonctions est nulle à \(x = 0\) et pourtant les trois possibilités sont exposées.,

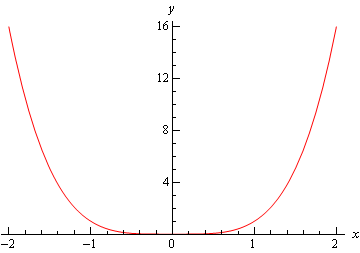
le premier est le graphe de \(f\left( x \right) = {x^4}\). Ce graphique a un minimum relatif à \(x = 0\).

Suivant est le graphe de \(f\left( x \right) = – {x^4}\) qui a un maximum relatif à \(x = 0\).

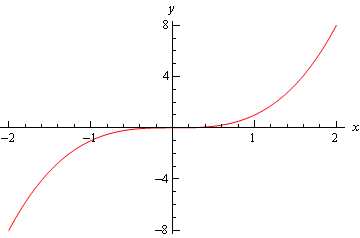
Enfin, il est le graphe de \(f\left( x \right) = {x^3}\) et de ce graphique n’avait ni par rapport minimum ou un maximum relatif à \(x = 0\).

Donc, nous pouvons voir que nous devons être prudents si nous tombons dans le troisième cas., Pour les moments où nous tombons dans ce cas, nous devrons recourir à d’autres méthodes de classification du point critique. Ceci est généralement fait avec le premier test dérivé.

revenons en arrière et regardons les points critiques du premier exemple et utilisons le Test de la dérivée seconde sur eux, si possible.

il nous faut travailler encore un exemple.