Mostrar aviso móvel mostrar todas as notas esconder todas as notas
Section 4-6 : The Shape of a Graph, Part II
in the previous section we saw how we could use the first derivative of a function to get some information about the graph of a function. Nesta seção nós vamos olhar para a informação que a segunda derivada de uma função pode nos dar uma sobre o gráfico de uma função.
Antes de fazermos isso, vamos precisar de algumas definições fora do caminho. O conceito principal que vamos discutir nesta secção é a concavidade. A concavidade é mais fácil de ver com um grafo (vamos dar a definição matemática em um bit).,
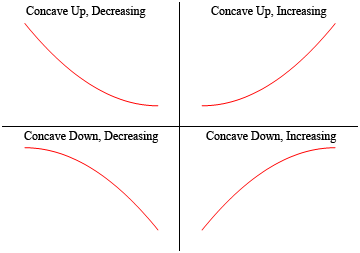
assim, uma função é côncava se “abre” para cima e a função é côncava se “abre” para baixo. Observe também que a concavidade não tem nada a ver com aumentar ou diminuir. Uma função pode ser côncava para cima e aumentar ou diminuir. Da mesma forma, uma função pode ser côncava para baixo e aumentar ou diminuir.
provavelmente não é a melhor maneira de definir a concavidade, dizendo de que maneira ela “abre” uma vez que esta é uma definição algo nebulosa. Aqui está a definição matemática de concavidade.,
Definição 1
para mostrar que os grafos acima de fato têm concavidade reivindicada acima aqui é o grafo novamente (explodido um pouco para tornar as coisas mais claras).
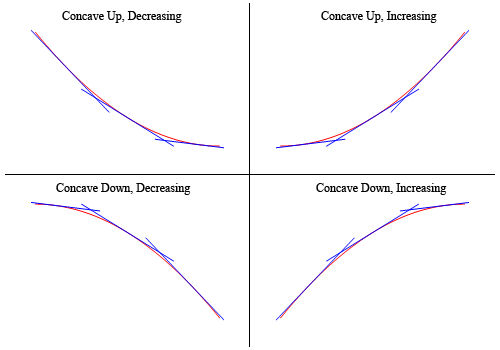
assim, como você pode ver, nos dois grafos superiores todas as linhas tangentes esboçadas estão todas abaixo do grafo da função e estas são côncavas para cima. Nos dois grafos inferiores, todas as linhas tangentes estão acima do grafo da função e estas são côncavas para baixo.,mais uma vez, observe que a concavidade e o aspecto crescente/decrescente da função são completamente separados e não têm nada a ver uns com os outros. Isto é importante de notar porque os alunos muitas vezes misturam estes dois e usam informações sobre um para obter informações sobre o outro.há mais uma definição que precisamos para sair do caminho.
Definição 2
Um ponto \(x = c\) é chamado de ponto de inflexão se a função é contínua no ponto e a concavidade do gráfico muda nesse ponto.,
Agora que temos todas as definições de concavidade fora do caminho que precisamos para trazer a segunda derivada para a mistura. Afinal de contas, começámos esta secção a dizer que íamos usar a segunda derivada para obter informações sobre o gráfico. O seguinte fato relaciona a segunda derivada de uma função à sua concavidade. A prova deste fato está na seção provas de aplicações derivadas do Capítulo Extras.
Fact
So, what this fact tells us is that the inflection points will be all the points were the second derivative changes sign., Vimos no capítulo anterior que uma função pode mudar Sinais se for zero ou não existir. Note que estávamos trabalhando com a primeira derivada na seção anterior, mas o fato de que uma função possivelmente mudando sinais onde ela é zero ou não existe não tem nada a ver com a primeira derivada. É simplesmente um fato que se aplica a todas as funções independentemente de serem derivadas ou não.,
isto, por sua vez, nos diz que uma lista de possíveis pontos de inflexão serão os pontos onde a segunda derivada é zero ou não existe, pois estes são os únicos pontos onde a segunda derivada pode mudar sinal.
tenha cuidado no entanto para não fazer a suposição de que só porque a segunda derivada é zero ou não existe que o ponto será um ponto de inflexão. Só saberemos que é um ponto de inflexão quando determinarmos a concavidade de ambos os lados. Só será um ponto de inflexão se a concavidade for diferente de ambos os lados do ponto.,
Agora que sabemos sobre concavidade podemos usar esta informação, bem como a informação crescente/decrescente da seção anterior para obter uma boa idéia de como um grafo deve se parecer. Vejamos um exemplo disso.
Podemos usar o exemplo anterior para ilustrar outra forma de classificar alguns dos pontos críticos de uma função como máximos relativos ou mínimos relativos.
como veremos em um pouco, precisaremos ter muito cuidado com \(x = 0\)., Neste caso, a segunda derivada é zero, mas isso não significa realmente que \(x = 0\) não é um mínimo relativo ou máximo. Veremos alguns exemplos disso em um pouco, mas precisamos obter algumas outras informações tratadas primeiro.
também é importante notar aqui que todos os pontos críticos neste exemplo foram pontos críticos em que a primeira derivada foi zero e isso é necessário para que isso funcione. Não seremos capazes de usar este teste em pontos críticos onde a derivada não existe.,
Aqui está o teste que pode ser usado para classificar alguns dos pontos críticos de uma função. A prova deste teste está na seção provas de aplicações derivadas do Capítulo Extras.
segundo ensaio derivado
a terceira parte do segundo ensaio derivado é importante de notar. Se a segunda derivada é zero, então o ponto crítico pode ser qualquer coisa. Abaixo estão os grafos de três funções todas as quais têm um ponto crítico em \(x = 0\), a segunda derivada de todas as funções é zero em \(x = 0\) e ainda assim todas as três possibilidades são exibidas.,
o primeiro é o grafo de \(f\esquerda (x \direita) = {x^4}\). Este gráfico tem um mínimo relativo em \(x = 0\).
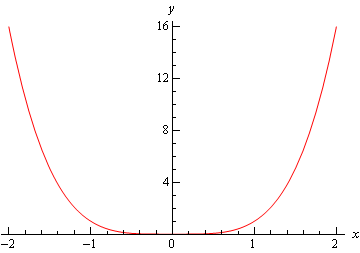
a seguir é o gráfico de \(f\esquerda( x \direita) = – {x^4}\) que tem um máximo relativo em \(x = 0\).

Finalmente, há o gráfico de \(f\left( x \right) = {x^3}\) e este gráfico não tinha nem um mínimo relativo ou um máximo relativo em \(x = 0\).
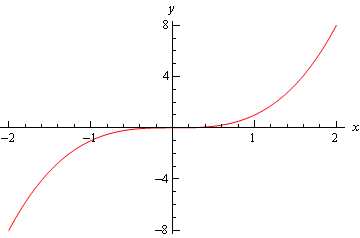
assim, podemos ver que temos de ter cuidado se caímos no terceiro caso., Para aqueles tempos em que caímos neste caso, teremos de recorrer a outros métodos de classificação do ponto crítico. Isto é geralmente feito com o primeiro teste derivado.
vamos voltar e dar uma olhada nos pontos críticos do primeiro exemplo e usar o segundo teste derivado sobre eles, se possível.vamos dar mais um exemplo.















