Good Mood

Imagine isto: você está fazendo uma apresentação de sua tese de Ph. D. sobre estabilidade em um dos seminários. Tudo corre bem, e finalmente, é o período de perguntas! E alguém do nada pergunta: “Qual é a diferença entre abordagem implícita e explícita?”! E já que estás a fazer estabilidade estática, nunca ouviste esses termos! Sim … já fiz isso!, Agora, eu sou um pouco mais sábio, então vamos dar uma olhada mais de perto nas diferenças entre Análise implícita e explícita

análise implícita e explícita diferem na abordagem à incrementação do tempo. Em análise implícita cada incremento de tempo tem que convergir, mas você pode definir incrementos de tempo bastante longos. Explicit on the other hand doesn’t have to converge each increment, but for the solution to be accurate time increments must be super small.isto parece muito simples, certo?, A menos que você comece a pensar sobre coisas como “qual devo usar” ou “quão pequeno deve ser o incremento de tempo explícito”, e coisas assim. Não te preocupes, eu cubro-te!vamos mergulhar!

dinâmica na sua melhor-implícita / explícita!

irá usar solucionadores implícitos e explícitos para resolver problemas dinâmicos. Isso significa que você não precisará saber essas coisas se você estiver fazendo análise estática., Se você não tiver certeza sobre a diferença entre análise estática e dinâmica, por favor leia este post primeiro – ele vai tornar as coisas mais fáceis de entender!

Dynamic analysis in a nutshell:

Dynamic analysis solves problems involving in inércia effects. Esses aparecem, quando as coisas mudam rapidamente em seu modelo (cargas aplicadas rapidamente, impactos, etc.). Engenheiros geralmente referem para isso como”dinâmica não linear”.

it should be noted, that often engineers call other analysis” dynamic ” as well., Coisas como análise Modal ou análise de resposta forçada que lidam com vibrações. Às vezes esses são chamados de “dinâmica linear”, mas geralmente é uma boa idéia para se certificar do que alguém quer dizer quando usa tal frase. Enquanto problemas” dinâmicos lineares ” são realmente interessantes, eu não vou discutir esses aqui. Você pode aprender mais sobre eles lendo este post!

a primeira coisa que realmente sinto que tenho que enfatizar é que solucionadores implícitos e explícitos resolvem os mesmos problemas!, Pense nisso não como” diferentes solucionadores”, mas como duas maneiras diferentes de resolver o mesmo problema.

em muitos casos, você pode usar solucionador implícito e explícito, e eles irão produzir o mesmo resultado. E acho que é por aqui que temos de começar!como funciona a análise dinâmica?

ambas as análises estão resolvendo um problema onde a velocidade das coisas é importante. Isto significa, na sua maioria, que a carga é aplicada muito rapidamente. Em tais casos, você sempre “iterate” sua carga no tempo., Basicamente, você vai usar o tempo para dizer ao solucionador “o que está acontecendo” e como a carga está mudando.

Em primeiro lugar, você tem que definir como a carga está mudando no tempo. Você geralmente faz isso usando gráficos, como o abaixo:

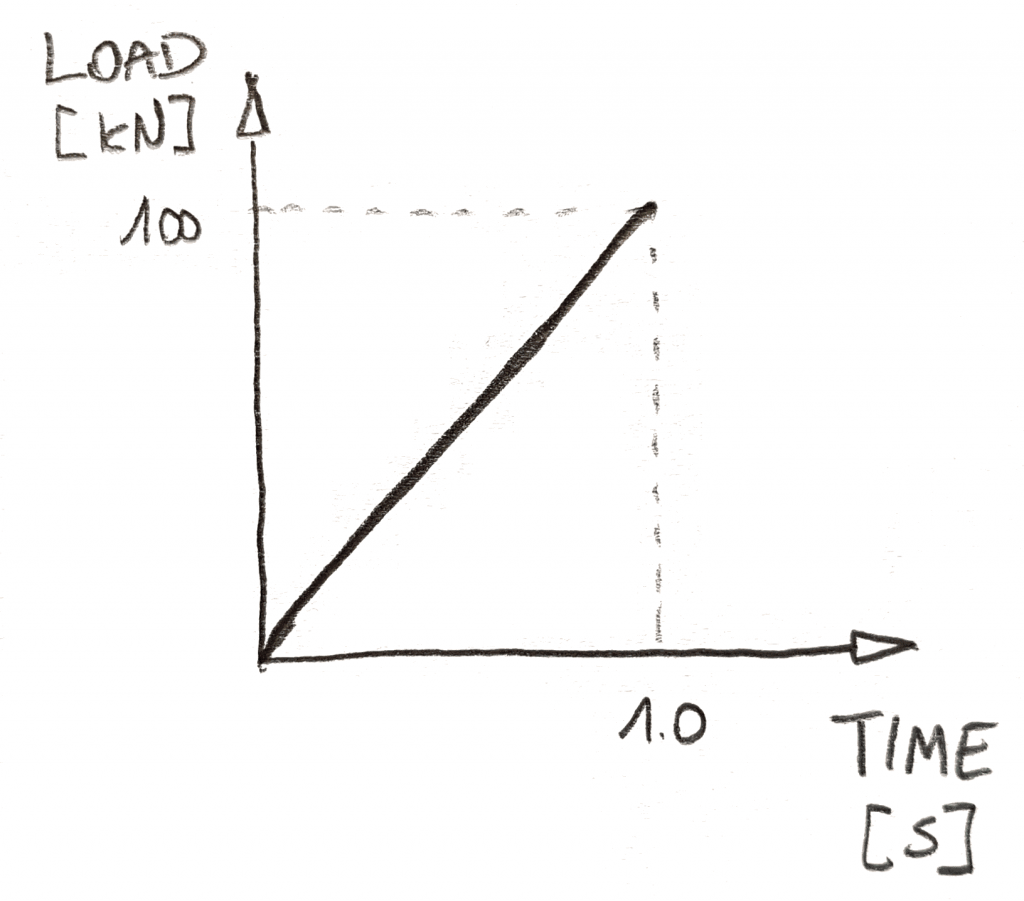
em análise dinâmica não linear, o tempo tem 2 papéis. Em primeiro lugar, ele permite que você diga ao solucionador, quando quanta carga deve ser aplicada. Você simplesmente tem que implementar cada carga com um gráfico dependente do tempo. Segundo … tempo é tempo! Ele diz ao solucionador o quão rápido as coisas estão indo!,

Imagine que você deseja ter como uma sequência de carga:

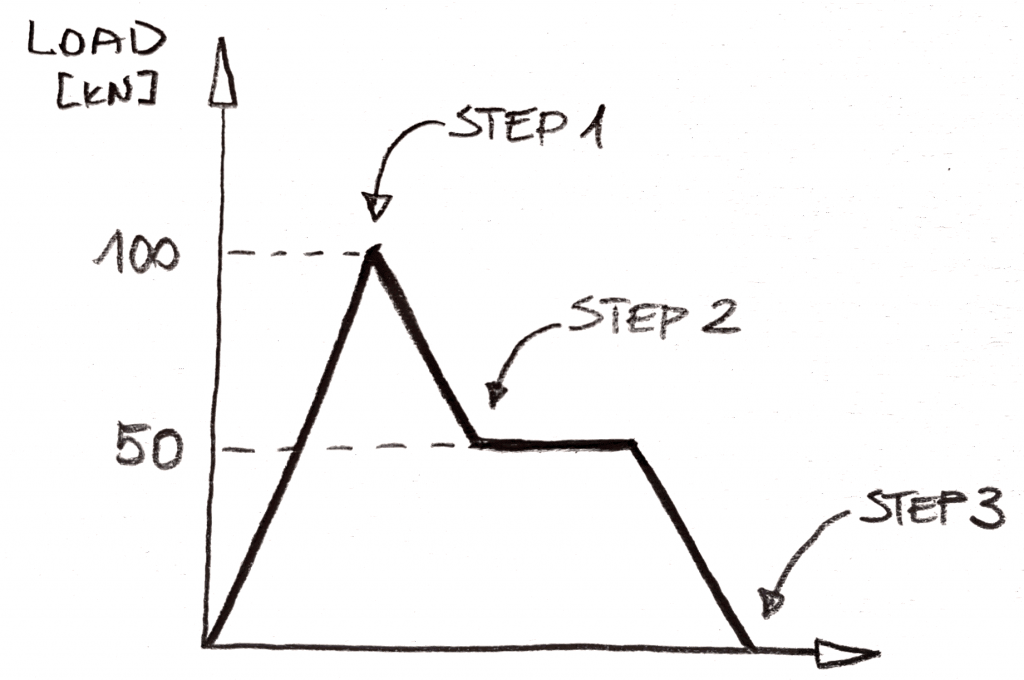
estáticos, este seria um 3 “passos” de análise (aqueles que são chamados subcases em NX Nastran, mas eu acho que Abaqus, na verdade, usou o “passo a passo” como um nome, não lembro isso para se embora!). A idéia seria simples, você tem que aplicar o 100kN de carga no Passo 1, em seguida, remover 50kN da carga no Passo 2, e remover 50kN no Passo 3. Não há maneira de incluir o” planalto ” de carga após o PASSO 2 na análise, e ele será omitido., A lógica é simples: sem mudanças na carga = nada muda na estática!

incrementos de Carga estática

Se o problema seria altamente não-linear, a carga seria uma “incrementada”. É raro ser capaz de aplicar ” carga completa “em análise não linear em”one go”! Normalmente, o solucionador aplicaria 1KN cada “incremento”. Isto significa que, após 100 incrementos, seria aplicada uma carga completa do Passo 1. Isso torna mais fácil para o solucionador convergir uma resposta correta.,

Existem também alguns algoritmos para modificar o aumento da carga durante a análise. Diferentes solucionadores querem que você defina isso de maneiras diferentes. Normalmente os pacotes da FEA usam multiplicadores de carga para isso. Isto significa que você pode dizer algo como: “em cada incremento aplicar 0,01 adicional de toda a carga”.

Awesome … but let’s get to dynamics, shall we?, Na análise dinâmica, você pode obter a distribuição de carga acima com uma carga de definição:

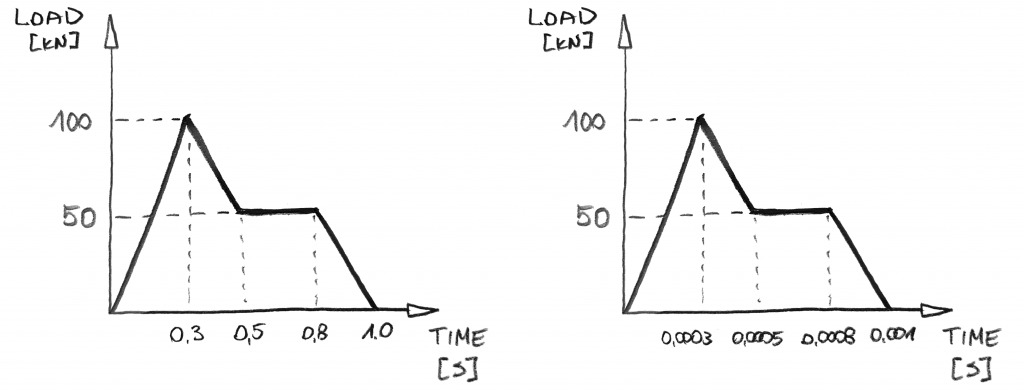
Instantaneamente, há algumas coisas que você pode observar:

• não Existem passos! Isto é porque na análise dinâmica você não vai aumentar a carga. Você vai aumentar o tempo! E como o tempo passa “constantemente “de zero para o valor prescrito, você pode incrementá-lo em”um passo”.

• O tempo é essencial! Quando se trata dos valores da carga, os gráficos acima são os mesmos., Mas este não é o mesmo caso dinâmico! O gráfico à direita aplica a carga 1000x mais rápido! Isso não é algo que você pode simplesmente ignorar em análise dinâmica!

em geral, quando você quer resolver um problema dinâmico, você está pedindo ao seu solucionador para fazer uma coisa. Você pede-lhe para calcular a série de incrementos de tempo, para ver o que está acontecendo no modelo. Em cada um desses incrementos, o tempo aumenta ligeiramente. Isto, naturalmente, também muda a carga no modelo. É por isso que você precisa ter um gráfico dependente do tempo para a carga., Assim, o solucionador “sabe” que Carga deve ser aplicada a cada incremento de tempo. Nesta medida, funciona da mesma forma que o aumento da carga na análise estática. O bônus é que, uma vez que você está aumentando o tempo, os efeitos de inércia podem ser levados em conta quando as coisas estão acontecendo rápido o suficiente.

nesta extensão, tanto a análise implícita quanto explícita faz mais ou menos a mesma coisa. Eles dividem o “tempo de análise” em pequenos incrementos, e então analisam o que está acontecendo em seu modelo um incremento de tempo após o outro. Mas aqui é onde as semelhanças terminam!, Você vê, há abordagens distintas para a incrementação do tempo que você pode ter!

implícito vs explícito-quando o tempo realmente importa!

acabou de aprender que, para calcular o problema dinâmico não linear, terá de aumentar progressivamente o “tempo de análise”. Como já referi, isto pode ser feito de duas formas.

I começará com a abordagem implícita. Eu acho que é mais fácil de entender, uma vez que ele funciona mais ou menos o mesmo que o aumento de carga em análise estática não-linear!,

como funciona a análise implícita:

em primeiro lugar, implícito parece ser uma solução mais “básica”. Em essência, ele funciona exatamente como você pensaria que deveria!

• em primeiro lugar, em cada incremento o “equilíbrio global” no modelo é estabelecido. Isto significa que cada incremento tem que convergir (isto está acontecendo em iterações).

• Após o equilíbrio global estar ok, o solucionador calcula todas as variáveis locais de elementos finitos (tensões, etc.) para este incremento.,

• benefícios: Uma vez que o equilíbrio global é verificado em cada incremento de tempo, esses incrementos podem ser grandes!
• desvantagens: cada incremento de tempo calcula lentamente, uma vez que iterações são necessárias para chegar ao equilíbrio global.

Se estiver familiarizado com a análise estática não linear, sentir-se-á “em casa” com a solução implícita. Como usuário, você geralmente começa a dizer o quão grande o tempo incrementos você quer ter. Esta é uma grande vantagem … que é fácil de perder., Porque solucionador explícito não oferece tal possibilidade!

Let’s take a look at explicit incrementation next!

How Explicit Analysis Works:

this one is funky. Funciona de uma maneira, que você não tem que convergir cada passo! Não há critérios de convergência a verificar e… não há iterações! Em vez de verificar o “equilíbrio global”, o solucionador assume que o equilíbrio “simplesmente existe”. Isto significa que a solução vai diretamente para o cálculo de variáveis locais de elementos finitos!, Como tal procedimento tem apenas um passo:

• calcular todas as variáveis locais de elementos finitos para um dado incremento, e passar para o próximo!

• benefícios: cada incremento calcula-se extremamente rápido!
• desvantagens: para isso funcionar, o passo de tempo tem que ser extremamente pequeno. Caso contrário, é impossível manter este equilíbrio que se supõe existir simplesmente. Para conseguir isso, o Usuário não tem controle direto sobre o tamanho dos incrementos em tempo real que o solucionador explícito tomará., O próprio solucionador calcula como os pequenos passos de tempo ainda estão ok. E esses incrementos de tempo aceitáveis são SUPER pequenos! É por isso que os problemas explícitos devem durar frações do segundo! Se durassem segundos… precisarias de milhões de incrementos!

para resumir rapidamente: ambos os solucionadores implícitos e explícitos resolvem a mesma coisa. A única diferença é como esses métodos aumentam o tempo.

tecnicamente, ambos devem produzir o mesmo resultado para todos os casos., Afinal, você pode analisar o mesmo problema com ambas as abordagens. Obviamente, a resposta não pode depender do método utilizado para resolver o problema! Mas é claro, você só vai escolher uma das abordagens para o seu próximo problema, então qual? Vamos descobrir!

o que é melhor para si: implícito ou explícito?

já concordámos que você pode usar solucionadores implícitos e explícitos para resolver o mesmo tipo de problemas. A única diferença está na aproximação à incrementação do tempo. Mas não é uma coisa trivial!, Se a diferença fosse pequena, ninguém se importaria de implementar ambos! Então vamos dar uma olhada em como este tempo incrementação influenciar as coisas!

ambos os solucionadores implícitos e explícitos têm algumas áreas onde brilham. E há uma sobreposição no seu uso:

• a análise implícita permite-lhe seleccionar a dimensão do incremento Temporal! Este incremento vai levar algum tempo para computar, uma vez que ele tem que iterar para o equilíbrio global primeiro. Mas você pode torná-lo “razoavelmente grande” para sua análise.,

• incrementos temporais explícitos calculam muito rapidamente! Simplesmente porque eles não interagem para o equilíbrio global… mas o aumento do tempo não é a sua escolha! O solucionador simplesmente assume que o incremento de tempo” aceitável “é” X ” e vai com ele. Note, que este ” X ” pode facilmente ser algo como 5e-7s… isto é super pequeno! Para resolver um problema que ocorre acima de 1s, você precisaria de 2 000 000 incrementos!

• e é isso! A velocidade da computação é exatamente a diferença entre implícita e explícita., Claro, o tamanho do passo explícito depende do seu modelo e os tempos de computação dependem do seu hardware. No entanto, existem observações simples que podemos facilmente fazer:

o Uso implícito de “slow análise”!

se a coisa que você calcula acontecer ao longo de vários segundos… não faz sentido usar o solucionador explícito. Vai levar uma eternidade para escavar os milhões de incrementos de tempo necessários para que isto possa computar!, Em vez disso, defina um passo de tempo” razoável ” para a análise implícita (digamos 100 incrementos de tempo iguais para a sua análise). Claro, cada um desses incrementos de tempo implícitos irá calcular muito mais do que um único incremento explícito. Mas não mais do que centenas de milhares deles!

o Uso explícito de “pesquisa rápida”! isto é óbvio, certo? Se o que você calcula acontecer na pequena fração de um segundo explícito é o seu amigo., Numa análise implícita, o seu incremento de tempo seria super pequeno … talvez até tão pequeno como o incremento na análise explícita. Em tal caso, a análise explícita será executada muito mais rápido, uma vez que não requer iterações de “equilíbrio global”. A análise implícita requer essas iterações (independentemente do passo de tempo!).

Entre coisas!

claro, existem problemas que acontecem no meio (como um impacto com velocidade de 5m/s)., Normalmente você pode resolver tal problema com ambos os solucionadores, mas pode ser irritante.

espero que isto o ajude a selecionar uma abordagem adequada aos seus problemas dinâmicos. Claro que, no final, a experiência é o melhor guia! Se você estiver em dúvida, execute alguns de seus problemas típicos em ambos implícitos e explícitos. Desta forma, você será capaz de comparar resultados (eles devem ser os mesmos). Mas o que é mais importante, você será capaz de comparar os tempos de computação! Isto lhe dará uma oportunidade de verificar, o que é uma abordagem melhor para você!,

quão explícito Adivinha o tamanho do passo de tempo?

Well, it’s all nice and dandy so far, but I think it would be nice to address one big issue. E isso é … se você não está selecionando o passo do Tempo em sua análise explícita… então quem o faz?

a explicação matemática exigiria uma discussão sobre a frequência natural máxima. Isto porque o incremento máximo de tempo” ainda aceitável ” é inversamente proporcional à frequência natural máxima. Tais cálculos podem ser feitos, é claro., Os resultados dependem da malha do modelo (quantos elementos existem, etc.). Mas nós não vamos lá, e há duas razões pelas quais: em primeiro lugar, eu não gosto de matemática (!). Em segundo lugar, não é assim que os solucionadores o fazem no final, embora esta seja a “maneira apropriada”.

o solucionador pode calcular a frequência natural máxima, é claro, mas isso leva bastante tempo. E uma vez que teria que ser feito em cada incremento de tempo explícito (pode haver muitos deles!) … yikes!, Felizmente, há uma maneira de estimar bem este valor, analisando cada elemento finito no sistema separadamente! A interpretação física deste estimativa (comumente usado na resolução de problemas) é:

o Máximo de incremento de tempo em análise explícita:

incremento de Tempo em análise explícita é muito curto. É o tempo em que uma onda elástica (ou seja, onda de impacto) pode viajar através de um único elemento finito do seu modelo. Claro, isso é verificado para todos os elementos finitos em seu modelo, e o menor tempo é selecionado.,

Como você pode ver, existem 2 componentes para o explícito componente de tempo de:

• Elástico da velocidade de onda (aka velocidade do som no material)! Isso depende apenas do material que você tem em seu modelo (e é diferente para diferentes materiais, é claro!). Você vai precisar do módulo e Jovem, densidade material e ração Poisson (em problemas 2D e 3D). É fácil encontrar tabelas que listam velocidades de onda elástica em vários materiais. Apenas para referência em aço, isto é cerca de 5200m / s (muitos metais são cerca de 4500-5500m/s).,

• Tamanho do elemento (e qualidade)! Tens a velocidade da onda, mas não é suficiente! Para saber o tempo que ele precisa para viajar através do elemento, você precisa saber o elemento “comprimento”. Embora isto seja super simples em elementos 1D (eles simplesmente têm comprimento), torna-se complicado em 2D e 3D. este comprimento não é “simplesmente” o mais curto dos elementos arestas, uma vez que os elementos podem ter uma geometria muito pobre. Há coisas que o solucionador faz para calcular isto. In 2D it could be an element area divided by the maximal edge length., Em 3D o pode significa que o volume do elemento é dividido pela área lateral máxima. É por isso que não só o tamanho do elemento, mas também os elementos qualidade é tão importante em análise explícita! Afinal… tudo o que você precisa é de um elemento pobre para realmente prejudicar o seu tempo de computação!

li algures que, embora a solução acima seja” precisa”, os solucionadores usam frequentemente” factores de segurança ” nisto. Se você obter um aumento de tempo maior do que a onda elástica “limite de velocidade” erros matemáticos ocorrem. Uma vez que as estimativas são usadas, os solucionadores muitas vezes reduzem o passo de tempo “apenas no caso”., Normalmente, o Fator de redução é de cerca de 0,9, mas isso pode variar de resolver para resolver, é claro.escala em massa!

No final, eu quero mencionar algo rapidamente.

você provavelmente notou, que o passo de tempo em explícito apenas depende da malha, Módulo jovem e densidade. Reduzir o módulo jovem pode não ser ideal, é claro, e você muitas vezes precisa de uma pequena malha para analisar detalhes. Mas em problemas “de baixa dinâmica” você pode tentar aumentar o passo de tempo explícito, aumentando a densidade material.,

This is called “mass scaling”. Os pacotes da FEA até oferecem soluções onde a densidade é aumentada apenas nos elementos que “decidem” sobre o incremento do tempo. Isto significa que, às vezes, apenas pequenas porções do seu modelo ficar mais pesado! Em algumas análises, você pode “escapar” com o aumento da massa de seu modelo. Se for esse o caso, isto pode ser uma solução para si. Apenas esteja ciente, que isso muda a forma como o seu modelo se comporta! Quando altas acelerações estão envolvidas, é melhor ter cuidado!

Resumo

Bom!, Você chegou aqui, obrigado por ler! Vamos acabar com isto, para que seja mais fácil de lembrar!

• análise dinâmica envolve tempo! Quando você aplica cargas, essas têm que ser definidas em uma função de tempo. Muitas vezes esta é uma relação linear. Mas isso não muda, que o tempo em que a carga é aplicada desempenha um papel significativo (especialmente se este tempo é curto!).

• 2 sabores de análise dinâmica! Você pode resolver os problemas dinâmicos “reais” com algoritmos implícitos e explícitos. Ambos estão bem, e nenhum deles é “melhor”., Mas devo dizer que o solucionador explícito faz parte de menos pacotes da FEA. Uma vez que nem todos os pacotes da FEA têm um, o solucionador explícito é visto como uma coisa “mais avançada”.

• o solucionador implícito é realmente bom se as coisas em sua análise acontecem relativamente lentamente. Digamos que a análise é mais do que 1s sem qualquer coisa abrupta acontecer durante esse tempo. A vantagem é que você pode escolher o tamanho do incremento de tempo que você quer. Mesmo que o único incremento leve mais tempo para calcular, há muito menos deles!,

• o solucionador explícito é ótimo para coisas rápidas acontecendo (digamos mais rápido do que 0,1 s). Você não pode escolher o incremento de tempo aqui – o solucionador irá configurá-lo automaticamente. Enquanto eles são geralmente super pequenos, pelo menos eles computam muito mais rápido do que os “implícitos”. O solucionador explícito calcula quão grande o incremento de tempo deve ser. Isso depende da velocidade do som em seu material, tamanho mínimo de elementos finitos(e qualidade do elemento!). Em alguns casos, você pode mudar a densidade (mesmo automaticamente apenas em “elementos decisivos”!) para ajustar este incremento Temporal., Isso funciona, porque a velocidade do som em seu material depende de sua densidade! Isto é chamado de “escala em massa”.